.

phần mềm tính tiền karaoke vietbill ⇔ kèo nhà cái hôm nay ⇔ Fun88

Giải vở bài tập Toán 7 chương I, bài 4: Luyện tập

Thứ năm - 24/10/2019 04:55
Hướng dẫn Giải vở bài tập Toán 7 chương I, bài 4: Luyện tập
a) Các phân số đã cho chưa tối giản, do đó ta hãy rút gọn chúng.
Ta có:
giai vbt toan 7 bai 4 cau 1
Bài 2:
Ta biết rằng số hữu tỉ dương lớn hơn 0; số hữu tỉ âm nhỏ hơn 0; trong hai số hữu tỉ âm số nào có giá trị tuyệt đối nhỏ hơn thì số đó lơn hơn. Do đó ta sắp xếp như sau:
- < -0,875 < 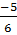 < 0 < 0,3 <

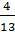Bài 3:
a. Ta có  < 1
              1 < 1,1
Suy ra:  < 1,1

b) Ta có -500 < 0
                    0 < 0,001
Suy ra:-500 < 0,001
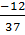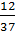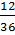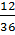c)  =  <  mà  =  nên - <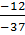
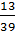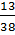 =  <  tức là  <
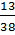Từ đó suy ra:  <

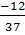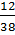Bài 4.
a) Áp dụng các tính chất giao hoán và kết hợp của phép nhân số hữu tỉ, ta có:
[ (-2,5). 0,38.0,4 ] - [0,125.3,15 . (-8)]
= [(-2,5.0,4). 0,38] – [-8.0,125). 3,15]
= (-l . 0,38) - (-1 .3,15)
= -0,38 + 3,15
= 2,77
b) Áp dụng tính chất phân phối của phép nhân đối với phép cộng, ta có:
[(-20,83). 0,2 + (-9,17) . 0,2] : [2,47.0,5 - (-3,53) . 0,5]
= [(-20,83 - 9,17). 0,2] : [(2,47 + 3,53). 0,5]
= (-30.0,2): (6.0,5)
= -6 : 3
= -2

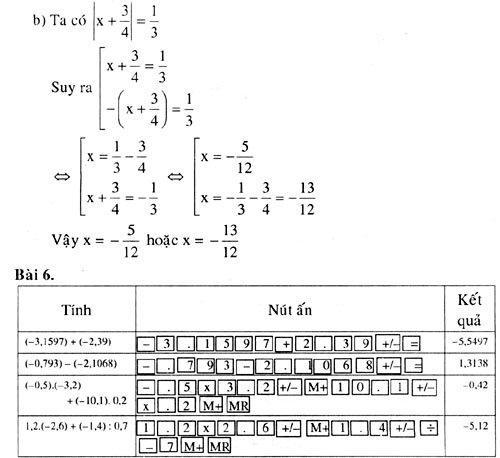
Bài 5.
Ta đã biết với mọi x ∈ Q ta luôn có |x| = |- x|. Do đó, ta giải như sau:
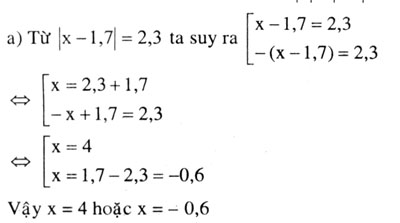
giai vbt toan 7 bai 4 cau 5a
giai vbt toan 7 bai 4 cau 6
Bản quyền bài viết thuộc về Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.

  Ý kiến bạn đọc

Theo dòng sự kiện

Xem tiếp...

Những tin mới hơn

Những tin cũ hơn

THÀNH VIÊN

Hãy đăng nhập thành viên để trải nghiệm đầy đủ các tiện ích trên site
Đăng ký
Kênh Bóng đá trực tiếp hôm nay miễn phí ⇔ Kênh 90Phut TV full HD ⇔ 888new ⇔ HM88 ⇔ F168 ⇔ 123b ⇔ 566 ⇔ 78Win ⇔ https://xn88.bio/ ⇔ SHBET ⇔ 78win ⇔ 66b ⇔ u888 ⇔ 888p ⇔ BL555 ⇔ f168 ⇔ Link MB66 ⇔ 8x bet ⇔ 789BET ⇔ LC88 ⇔ 999slot ⇔ 789F ⇔ 8xbet ⇔ https://789betcom0.com/ ⇔ https://hi88.baby/ ⇔ 789BET ⇔ go8 ⇔ ev99 ⇔ go88 ⇔ Kkwin ⇔ tv88 ⇔ 89bet ⇔ 88go ⇔ 188v ⇔ f168 ⇔ QQ88 ⇔ bk8 ⇔ bk8 ⇔ 99ok ⇔ iwinclub ⇔ vn88 ⇔ 69vn ⇔ m88 ⇔ 56win ⇔ RWIN ⇔ 888new ⇔ BL555 ⇔ hi88 ⇔ https://fun88.social/ ⇔ thabet ⇔ https://qq88.fun/ ⇔ 888New ⇔ SHBET ⇔ keo nha cai ⇔ https://bshbet.com/ ⇔ https://uk88.rocks ⇔ RR88 ⇔ 188v ⇔ 78win ⇔ https://hello8880.net/ ⇔ mb 66 ⇔ TV88 ⇔ ek333 ⇔ xoso66 ⇔ X88 ⇔ tt88 ⇔ 88i ⇔ KINGFUN ⇔ https://789club24.com/ ⇔ https://98winlive.com/ ⇔ Game bài đổi thưởng ⇔ https://bet88yk.com/ ⇔ https://alo789apk.app/ ⇔ https://33win100.com/ ⇔ https://u888ny.com/ ⇔ alo789 ⇔ https://hello880.net/ ⇔ https://789club60.com/ ⇔ https://blc88.net/ ⇔ 23win ⇔ uu88 ⇔ xoso66 ⇔ bomwin ⇔ https://789club24.com/ ⇔ dola789 ⇔ 8xbet ⇔ XX88 ⇔ 69vn ⇔ Uu88 ⇔ win456 ⇔ Tài xỉu online ⇔ XN88 ⇔ https://33win101.com/ ⇔ Slot365 ⇔ bet88 ⇔ XX88 ⇔ VN88 ⇔ 789BET ⇔ OKFUN ⇔ hitclub ⇔ Kkwin ⇔ VankhanhTV ⇔ XN88 ⇔ KUWIN ⇔ 58WIN ⇔ 68 game bài ⇔ https://taixiu88.pro/ ⇔ 888new.lol ⇔ OK9 ⇔ K8CC ⇔ https://hi88.gives/ ⇔ 68 game bài ⇔ https://shbetk.net/ ⇔ https://mm88.us.com/ ⇔ 79king ⇔ ww88 ⇔ https://78win.bot/ ⇔ https://lc88o.com/ ⇔ https://hi88.uno/ ⇔ https://58win1.info/ ⇔ j88 ⇔ j88 ⇔ 69vn ⇔ Slot365 ⇔ 888TO ⇔ wstar77 ⇔ 73bet ⇔ 11uu ⇔ 78win ⇔ Slot365 ⇔ mv88 ⇔ Bsport ⇔ 888New ⇔ EV99 ⇔ u88 ⇔ BIN88 ⇔ https://f8bet0.world ⇔ https://qq88.studio/ ⇔ https://nh8811.com/ ⇔ Leo88 ⇔ EV99 ⇔ 3win ⇔ https://cakhiatv88.net/ ⇔ hi88 ⇔ 888To ⇔ 789pu.com ⇔ hi88 ⇔ au88 ⇔ 555WIN ⇔ https://f168hi.com/ ⇔ sv66 ⇔ ax88 ⇔ https://32win.vc/ ⇔ PG88 ⇔ PG88 ⇔ EE88 ⇔ QQ88 ⇔ Vin777 ⇔ SV388 ⇔ 23WIN ⇔ https://vankhanhtvv.com/ ⇔ Nhà Cái LC88 ⇔ https://f168.tech/ ⇔ https://8kbetbh.com/ ⇔ https://bong99.onl/ ⇔ 123B ⇔ https://rr88.com.se/ ⇔ https://sunwinn.deal/ ⇔ https://bong88vn.wiki/ ⇔ https://shbet.racing/ ⇔ RR99 ⇔ Mv88 ⇔ BL555 ⇔ hi88com ⇔ https://w88link1.com/ ⇔ xocdia88 ⇔ vuabet88 ⇔ betvisa ⇔ KJC ⇔ Go8 ⇔ thabet ⇔ BET88 ⇔ 58Win ⇔ 69VN ⇔ 789win ⇔ 89bet ⇔ 6ff ⇔ https://luck8.ph/ ⇔ 888slot ⇔ 566 ⇔ https://qq88.co.com/ ⇔ https://j888.us.com/ ⇔ ww88 ⇔ 789WIN ⇔ W88 ⇔ UU88 ⇔ Lc 88 ⇔ TD88 ⇔ https://nohu90i.net/ ⇔ 78Win ⇔ 33win ⇔ https://okwins.vip/ ⇔ 122bet ⇔ 881bet ⇔ xoilac xin ⇔ e2bet ⇔ F168 ⇔ https://go8d.com/ ⇔ luck8 ⇔ https://x88casino.net/ ⇔ sunwin ⇔ https://kjc.events/ ⇔ https://79kings.blue/ ⇔ DR88 ⇔ DR88 ⇔ DR88 ⇔ DR88 ⇔ SHBET ⇔ CM88 ⇔ 888p ⇔ OKFUN ⇔ https://32win.cool/ ⇔ Hb88 ⇔ Bong88 ⇔ https://3winn.in.net/ ⇔ Fun88 ⇔ kkwin ⇔ https://kkwin.fan/ ⇔ win678 ⇔ x88 ⇔ https://j88gg.com/ ⇔ https://u88886.com/ ⇔ LC88 Vip ⇔ 68win ⇔ LC88 ⇔ 79king ⇔ https://hitclub88.us/ ⇔ New88 ⇔ https://fun88link0.com/ ⇔ https://fun88link1.com/ ⇔ https://188betlink0.com/ ⇔ https://188betlink1.com/ ⇔ https://188betlink2.com/ ⇔ https://w88link0.com/ ⇔ thabet ⇔ 888P ⇔ 11UU ⇔ EV88 ⇔ 789F ⇔ 69vn ⇔ 77win ⇔ xx88 ⇔ 78win ⇔ https://okfun.bz/ ⇔ https://daga88.beer/ ⇔ QQ88 ⇔ https://i9betz4.com/ ⇔ Kuwin ⇔ w88link2.com ⇔ w88link3.com ⇔ 32WIN ⇔ https://8dayvip.mobi/ ⇔ https://8dayvip.com/ ⇔ 86bet ⇔ t88 ⇔ af88 ⇔ U888 ⇔ 86bet ⇔ https://pg99yk.com/ ⇔ https://u888wl.com/ ⇔ kingfun ⇔ 888new ⇔ 88AA ⇔ GK88 ⇔ https://78wincom.net/ ⇔ GO99 ⇔ BET88 ⇔ 99win ⇔ TT88 ⇔ https://8kbettt.com/ ⇔ https://86bet.tech/ ⇔ https://789betca.com/ ⇔ https://fly88.gifts/ ⇔ lc88 ⇔ VN88 ⇔ 69vn ⇔ nh88 ⇔ vn88 ⇔ tv88 ⇔ 88vv ⇔ tỷ lệ kèo nhà cái 88 ⇔ PG66 ⇔ 68win ⇔ SV388 ⇔ SHBET ⇔ MAX79 ⇔ HM88 ⇔ TV88 ⇔ https://bet88.ventures/ ⇔ zx88 ⇔ https://f168.name/ ⇔ https://kjc.ac/ ⇔ link vn88 ⇔ HZ88 ⇔ Bet88 ⇔ XN88 ⇔ VN23 ⇔ https://555win.bike/ ⇔ 789f ⇔ Hitclub ⇔ https://f8bet80.one/ ⇔ https://okfun.center/ ⇔ https://hi88.tours/ ⇔ https://new88blog.org ⇔ https://uu88vn.com ⇔ 69VN ⇔ Ok365 ⇔ 6FF ⇔ Nohu90 ⇔ go8 ⇔ 22vip ⇔ 86bet ⇔ https://go8.beer/ ⇔ sin88 ⇔ 9win ⇔ 88i ⇔ https://u888.ac/ ⇔ https://king88com.uk.net/ ⇔ https://shbet.gg/ ⇔ LC88 ⇔ OKKING ⇔ 13win ⇔ https://88fc0.com/ ⇔ abc8 ⇔ U888 ⇔ https://s666.garden ⇔ https://fly88.select/ ⇔ https://bk8co.net/ ⇔ bet88 ⇔ F168 ⇔ https://qq8876.net/ ⇔ hi88s com ⇔ f168 ⇔ https://88xx.mobi/ ⇔ bet88 ⇔ 88clb ⇔ GO8 ⇔ https://qq88.social/ ⇔ LC88 ⇔ https://j88vm.com/ ⇔ https://78winvina.com/ ⇔ https://luongson161.tv/ ⇔ ⇔ https://okfun.cfd/ ⇔ https://keonhacai.deals/ ⇔ https://j88com.today/ ⇔ 28bet ⇔ MB66 ⇔ https://mk8th.net/ ⇔ https://58win.faith/ ⇔ Jun88 ⇔ 188v ⇔ https://s8.surf/ ⇔ https://jun88.school/ ⇔ https://qq887p.com/ ⇔ https://hi88.biz/ ⇔ https://mk8.ac/ ⇔ 78win ⇔ motphimchill ⇔ SHBET ⇔ x88 ⇔ https://mb668.co/ ⇔ https://f168.law/ ⇔ https://saobet.shop/ ⇔ win678 ⇔ https://8kbetnh.com/ ⇔ https://j8kbet.com/ ⇔ 33win ⇔ https://xx88tv.com/ ⇔ i9 Bet ⇔ kèo nhà cái ⇔ S666 ⇔ BL555 ⇔ max79 ⇔ bl-555.site ⇔ https://8scom.dev/ ⇔ https://f168.us/ ⇔ au88 ⇔ lc88 ⇔ https://tp88.help/ ⇔ 8kbet ⇔ TT88 ⇔ ev99 ⇔ vn168 ⇔ U888 ⇔ okking ⇔ j88 ⇔ https://32win.football/ ⇔ 789P ⇔ 28bet ⇔ 32 win ⇔ https://nohu.com.mx/ ⇔ https://789fnew.com/ ⇔ xin88 ⇔ 88GO ⇔ tv88 ⇔ LC88 ⇔ https://five88.meme/ ⇔ https://13win.vegas/ ⇔ S8 ⇔ 32win ⇔ Kuwin ⇔ https://hitclubhq.com/ ⇔ https://qq88.media/ ⇔ 888vi ⇔ https://keonhacai1.us.com/ ⇔ tt88 ⇔ mn88 ⇔ https://789winst.com/ ⇔ BL555 ⇔ HM88 ⇔ LC88 ⇔ QQ88 ⇔ mb66 ⇔ 88AA ⇔ aalo789 ⇔ PG99 ⇔ PG88 ⇔ QQ88 ⇔ https://s888.baby/ ⇔ 100vip ⇔ E2bet ⇔ F168 ⇔ tr88 ⇔ 888P ⇔ 8xbet ⇔ rr88vip ⇔ https://jun88.black/ ⇔ x88 ⇔ Nhà Cái LC88 ⇔ sv66 ⇔ 789win ⇔ 161bet ⇔ alo789 ⇔ EE88 ⇔ Abc8 ⇔ Sunwin ⇔ SV388 ⇔ S666 đăng nhập ⇔ Nhà cái vn88 ⇔ 89BET ⇔ SUN WIN ⇔ https://98wina1.com/ ⇔ tv88 ⇔ 789f ⇔ bong88 ⇔ sky88 ⇔ abc8 ⇔ good88 ⇔ Cổng game rikvip ⇔ https://u888n.info/ ⇔ https://98winwi.com/ ⇔ hi88 ⇔ 888p ⇔ Bet88 ⇔ MM88 ⇔ https://88hello88vina.com/ ⇔ https://888baz.com/ ⇔ 56win ⇔ 56win ⇔ 888p ⇔ AF88 ⇔ w188 ⇔ SC88 ⇔ S666 ⇔ 77WIN ⇔ CM88 ⇔
Bạn đã không sử dụng Site, Bấm vào đây để duy trì trạng thái đăng nhập. Thời gian chờ: 60 giây