Câu 1 - Trang 7: (Toán 6 tập 1 sách Cánh Diều)
Liệt kê các phần tử của mỗi tập hợp sau:
a) A là tập hơp các hình trong Hình 3;

b) B là tập hợp các chữ cái xuất hiện trong từ "NHA TRANG";
c) C là tập hợp các tháng của Quý II (biết một năm gồm 4 quý);
d) D là tập hợp các nốt nhạc có trong khuông nhạc Hình 4;
 Giải:
Giải:
a) Quan sát Hình 3, ta thấy các hình (ta đã được học ở Tiểu học) theo thứ tự từ trái qua phải là: hình chữ nhật; hình vuông; hình bình hành; hình tam giác; hình thang.
Do đó ta viết tập hợp A là:
A = {hình chữ nhật; hình vuông; hình bình hành; hình tam giác; hình thang}.
b) Ta thấy các chữ cái xuất hiện trong từ "NHA TRANG" là: N; H; A; T; R; A; N; G, trong đó các chữ cái N; A xuất hiện hai lần. Mà ta đã biết, trong tập hợp mỗi phần tử được liệt kê một lần (nội dung kiến thức Trang 5/SGK).
Do đó ta viết tập hợp B là:
B = {N; H; A; T; R; G}.
c) Ta đã biết một năm gồm bốn quý, mỗi quý gồm ba tháng liên tiếp nhau (tính từ tháng đầu tiên của năm) như sau:
Quý I: tháng 1; tháng 2; tháng 3
Quý II: tháng 4; tháng 5; tháng 6
Quý III: tháng 7; tháng 8; tháng 9
Quý IV: tháng 10; tháng 11; tháng 12
Do đó, ta viết tập hợp C gồm tên các tháng của Quý II là:
C = {tháng 4; tháng 5; tháng 6}.
d) Quan sát Hình 4, ta thấy tên các nốt nhạc theo thứ tự từ trái qua phải lần lượt là: Đồ; Rê; Mi; Pha; Son; La; Si.
Do đó ta viết tập hợp D như sau:
D = {Đồ; Rê; Mi; Pha; Son; La; Si}.
Câu 2 - Trang 7: (Toán 6 tập 1 sách Cánh Diều)
Cho tập hợp A = {11; 13; 17; 19}. Chọn kí hiệu "∈","∉" thích hợp vào chỗ chấm:
a) 11 .......... A
b) 12 ........... A
c) 14 .......... A
d) 19 ........... A
Giải:
a) Ta thấy tập hợp A chứa số 11 hay 11 thuộc tập hợp A nên ta viết: 11 ∈ A
b) Ta thấy tập hợp A không chứa 12 hay 12 không thuộc tập hợp A nên ta viết: 12 ∉ A;
c) Ta thấy tập hợp A không chứa 14 hay 14 không thuộc tập hợp A nên ta viết: 14 ∉ A;
d) Ta thấy tập hợp A chứa số 19 hay 19 thuộc tập hợp A nên ta viết: 19 ∈ A.
Câu 3 - Trang 8: (Toán 6 tập 1 sách Cánh Diều)
Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của tập hợp đó:
a, A = {x | x là số tự nhiên chẵn, x < 14}
b, B = {x | x là số tự nhiên chẵn, 40 < x < 50}
c, C = {x | x là số tự nhiên lẻ, x < 15}
d, D = {x | x là số tự nhiên lẻ, 9 < x < 20}
Giải:
a) A = {x | x là số tự nhiên chẵn, x < 14}
Ta thấy tập hợp A gồm các số tự nhiên chẵn nhỏ hơn 14 nên các phần tử thuộc tập hợp A là: 0; 2; 4; 6; 8; 10; 12.
Vậy ta viết tập hợp A là:
A = {0; 2; 4; 6; 8; 10; 12}.
b) B = {x | x là số tự nhiên chẵn, 40 < x < 50}
Ta thấy tập hợp B gồm các số tự nhiên chẵn lớn hơn 40 và nhỏ hơn 50 nên các phần tử thuộc tập hợp B là: 42; 44; 46; 48.
Vậy ta viết tập hợp B là:
B = {42; 44; 46; 48}.
c) C = {x | x là số tự nhiên lẻ, x < 15};
Ta thấy tập hợp C là các số tự nhiên lẻ nhỏ hơn 15 nên các phần tử thuộc tập hợp C là 1; 3; 5; 7; 9; 11; 13.
Do đó ta viết tập hợp C là:
C = {1; 3; 5; 7; 9; 11; 13}.
d) D = {x | x là số tự nhiên lẻ, 9 < x < 20}.
Ta thấy tập hợp D là các số tự nhiên lẻ lớn hơn 9 và nhỏ hơn 20 nên các phân tử thuộc tập hợp D là: 11; 13; 15; 17; 19.
Do đó ta viết tập hợp D là:
D = {11; 13; 15; 17; 19}.
Câu 4 - Trang 8: (Toán 6 tập 1 sách Cánh Diều)
Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó:
a) A = {0; 3; 6; 9; 12; 15}
b) B = {5; 10; 15; 20; 25; 30}
c) C = {10; 20; 30; 40; 50; 60; 70; 80; 90}
d) D = {1; 5; 9; 13; 17}.
Giải:
a) A = {0; 3; 6; 9; 12; 15};
Ta thấy các số 0; 3; 6; 9; 12; 15 là các số tự nhiên chia hết cho 3 và nhỏ hơn 16 nên ta viết tập hợp A bằng cách chỉ ra tính chất đặc trưng là:
A = {x | x là số tự nhiên chia hết cho 3, x < 16}.
b) B = {5; 10; 15; 20; 25; 30};
Ta thấy các số 5; 10; 15; 20; 25; 30 là các số tự nhiên chia hết cho 5, lớn hơn 0 và nhỏ hơn 31 (hoặc ta có thể viết nhỏ hơn 32; …; 35).
Vậy ta có thể viết tập hợp B bằng các cách sau:
Cách 1:
B = {x | x là các số tự nhiên chia hết cho 5, 0 < x < 31}.
Cách 2:
B = {x | x là các số tự nhiên chia hết cho 5, 0 < x < 35}…
c) C = {10; 20; 30; 40; 50; 60; 70; 80; 90};
Ta thấy các số 10; 20; 30; 40; 50; 60; 70; 80; 90 là các số tự nhiên chia hết cho 10, lớn hơn 0 và nhỏ hơn 100 (hoặc ta có thể viết nhỏ hơn 91; …; 99).
Vậy ta có thể viết tập hợp C bằng các cách sau:
Cách 1:
C = {x | x là các số tự nhiên chia hết cho 10, 0 < x < 91}.
Cách 2:
C = {x | x là các số tự nhiên chia hết cho 10, 0 < x < 100}…
d) D = {1; 5; 9; 13; 17}
Ta thấy các số 1; 5; 9; 13; 17 là các số tự nhiên thỏa mãn số sau hơn số trước 4 đơn vị (hay còn gọi là hơn kém nhau 4 đơn vị), lớn hơn 0 và nhỏ hơn 18.
Do đó ta viết tập hợp D là:
D = {x | x là các số tự nhiên hơn kém nhau 4 đơn vị, 0 < x < 18}.
 Câu 1 - Trang 8: (Toán 6 tập 1 sách Cánh Diều)
Câu 1 - Trang 8: (Toán 6 tập 1 sách Cánh Diều)
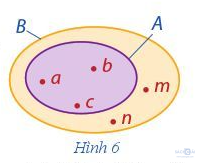
a) Viết tập hợp A, B được minh họa bởi Hình 6 bằng cách liệt kê các phần tử của tập hợp.
b) Quan sát Hình 6 và cho biết phát biểu nào sau đây là đúng:
1. a ∉ B;
2. m ∈ A;
3. b ∈ B;
4. n ∉ A.
Giải:
a) Ta thấy trong biểu đồ Ven minh họa tập hợp A, các phần tử a, b, c nằm trong vòng kín
Vậy ta viết tập hợp A là: A = {a; b; c}.
Tương tự, ta thấy các phần tử a, b, c, m, n đều nằm trong vòn kín của biểu đồ Ven minh họa tập hợp B
Do đó ta viết tập hợp B là: B = {a; b; c; m; n}.
b) Ta thấy,
+ Tập hợp B chứa phần tử A nên a ∈ B nên 1 sai.
+ Tập hợp A không chứa phần tử m nên m ∉ A nên 2 sai.
+ Tập hợp B chứa phần tử B nên b ∈ B nên 3 đúng.
+ Tập hợp A không chứa phần tử n nên n ∉ A nên 4 đúng.
Vậy phát biểu 3 và 4 là phát biểu đúng.
Câu 2 - Trang 8: (Toán 6 tập 1 sách Cánh Diều)
Tất cả học sinh của lớp 6A đều biết chơi bóng rổ hoặc cờ vua. Số học sinh biết chơi bóng rổ là 20, số học sinh biết chơi cờ vua là 35. Số học sinh của lớp 6A nhiều nhất là bao nhiêu?
Giải:
Do tất cả các học sinh của lớp 6A đều biết chơi bóng rổ hoặc cờ vua nên số học sinh lớn nhất của 6A là:
20 + 35 = 55 (học sinh)
Vậy số học sinh của lớp 6A nhiều nhất là 55 học sinh.