Đồ thị trong Pascal
2020-08-08T10:06:51-04:00
2020-08-08T10:06:51-04:00
https://sachgiai.com/Tin-hoc/do-thi-trong-pascal-13461.html
https://sachgiai.com/uploads/news/2020_08/do-thi-trong-pascal-4.jpg
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Thứ bảy - 08/08/2020 09:49
Trong nhiều tình huống, chúng ta thường vẽ những sơ đồ, trong đó có những sơ đồ gồm những điểm biểu thị các đối tượng được xem xét (người, tổ chức, đội bóng, thành phố...) và nối một số điểm với nhau bằng những đoạn cong hoặc thẳng tượng trưng cho quan hệ nào đó giữa các đối tượng.
1. TỔNG QUÁT
Trong nhiều tình huống, chúng ta thường vẽ những sơ đồ, trong đó có những sơ đồ gồm những điểm biểu thị các đối tượng được xem xét (người, tổ chức, đội bóng, thành phố...) và nối một số điểm với nhau bằng những đoạn cong hoặc thẳng tượng trưng cho quan hệ nào đó giữa các đối tượng. Các sơ đồ như vậy được dùng khắp nơi: sơ đồ mạng điện, sơ đồ tổ chức, sơ đồ giao thông... Đó là những ví dụ về Graph. Một Graph là một tập hợp hữu hạn các điểm (gọi là đỉnh của Graph) cùng với tập hợp các đoạn đường cong hay thẳng (gọi là cạnh của Graph) có các đầu mút tại các đỉnh của Graph.
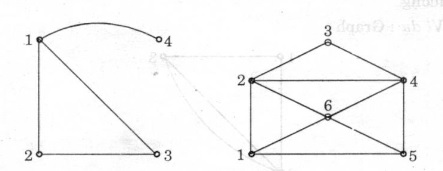
■ Ví dụ:
 2. BIỂU DIỄN GRAPH
Có nhiều cách biểu diễn Graph, ở đây ta chỉ xét một cách biểu diễn đơn giản, đó là dùng một mảng vuông hai chiều (ma trận) có kiểu phần tử là Boolean:
A[1..n, 1..n) of Boolean
Trong đó:
• n: chỉ số đỉnh của Graph
• A[i, j]: TRUE (1) nếu giữa đỉnh i và j có cạnh nối.
• A[i, j]: FALSE (0) nếu giữa đỉnh j không có cạnh nối.
A thường được gọi là ma trận nối của Graph G.
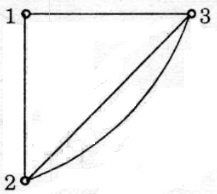
■ Ví dụ: Graph
2. BIỂU DIỄN GRAPH
Có nhiều cách biểu diễn Graph, ở đây ta chỉ xét một cách biểu diễn đơn giản, đó là dùng một mảng vuông hai chiều (ma trận) có kiểu phần tử là Boolean:
A[1..n, 1..n) of Boolean
Trong đó:
• n: chỉ số đỉnh của Graph
• A[i, j]: TRUE (1) nếu giữa đỉnh i và j có cạnh nối.
• A[i, j]: FALSE (0) nếu giữa đỉnh j không có cạnh nối.
A thường được gọi là ma trận nối của Graph G.
■ Ví dụ: Graph
 có ma trận nối là:
có ma trận nối là:
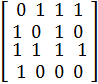 - Nếu tồn tại i, j sao cho A[i, j] ≠ A[j, i] thì Graph G sẽ được coi là có hướng.
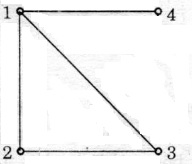
■ Ví dụ: Graph
- Nếu tồn tại i, j sao cho A[i, j] ≠ A[j, i] thì Graph G sẽ được coi là có hướng.
■ Ví dụ: Graph
 có ma trận nối là:
có ma trận nối là:
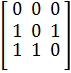 - Nếu có độ dài Lij của đường đi từ đỉnh i đến đỉnh j thì ta có thể lập thêm ma trận độ dài L[1..n, 1..n] như sau:
L[i, j] = Lij
3. KIỂM TRA XEM CÓ ĐƯỜNG ĐI TỪ ĐỈNH Đ ĐẾN ĐỈNH C TRÊN MỘT ĐỒ THỊ CÓ HƯỚNG HAY KHÔNG
a) Bài toán
Cho đồ thị có hướng G có ma trận nối là A và hai đỉnh Đ, C của G. Hãy tìm xem có đường đi từ Đ đến C không.
b) Thuật toán
- Dùng mảng C[1..n] of Boolean để đánh dấu các đỉnh đã đi qua.
- Dùng procedure lantu(i) một cách đệ qui để lan từ đỉnh Đ đến một đỉnh nào đó có thể được, rồi từ đó lại lan tiếp đến các đỉnh khác chưa lan tới cho đến khi gặp đỉnh thì biến Boolean kq cho kết quả true nghĩa là có đường đi.
c) Thể hiện bằng PASCAL
Procedure Lantu (i: byte);
Var j: byte;
Begin
if (i = c) then kq := True
else
Begin
For j := 1 to n do
if A[i, j] and not c[j] then
Begin
c[j] := true;
lantu (j);
end;
end;
end;
Begin {chương trình chính}
Kq := False;
For j := 1 to n do C[j] := False;
lantu (Đ);
if kq then writeln ('có đường đi');
else writeln ('không có’);
end.
4. TÌM ĐƯỜNG ĐI NGẮN NHẤT
a) Bài toán
Tìm đường đi ngắn nhất từ đỉnh nguồn (1) đến một đỉnh khác (j) của một đồ thị có hướng G có ma trận nôi là A và ma trận độ dài L chứa chiều dài các cung:
L[i, i] = 0 với mọi i = 1 ... n
L[i, j] >= 0 nếu tồn tại cung từ đỉnh i đến đỉnh j.
L[i, j] = ∞ nếu không tồn tại cung từ đỉnh i đến đỉnh j.
b) Thuật toán (Dijkstra)
- Nguyên lí chính của thuật toán này là: Nếu tồn tại đường đi ngắn nhất từ đỉnh i đến đỉnh j và đỉnh k ở trên đường đi này thì k sẽ chia đường đi thành hai đoạn và hai đoạn đó phải là hai đoạn ngắn nhất nối từ i đến k và từ k đến j.
Ta dùng hai mảng C và S.
C: chứa các đỉnh chưa được chọn.
S: chứa các đỉnh đã được chọn.
- Tại mỗi thời điểm tập S chứa các đỉnh mà khoảng cách nhỏ nhất từ đỉnh nguồn đến, chúng đã được xác định tập C chứa các đỉnh còn lại.
- Bắt đầu S = {Đỉnh nguồn}
- Kết thúc := tập các đỉnh của G.
- Tại mỗi bước ta chọn một đỉnh C mà khoảng cách D[x] từ đỉnh nguồn đến X là nhỏ nhất.
- Ta nói rằng đường đi từ đỉnh nguồn đến một đỉnh khác là đặc biệt nếu tất cả các đỉnh trung gian trên đường đi này đều ở trong tập s.
- Tại mỗi bước của thuật toán có mảng một chiều D chứa chiều dài của đường đi đặc biệt ngắn nhất đến mỗi đỉnh của đồ thị.
- Mỗi lần ta đưa đỉnh X mới vào s đường đi riêng biệt ngắn nhất đến X cũng chính là đường đi ngắn nhất trong tất cả các đường đi đến X.
- Khi thuật toán kết thúc, tất cả các đỉnh của G đều thuộc S suy ra mọi đường đi từ nguồn đến các đỉnh đều là đặc biệt.
- Ví dụ:
- Nếu có độ dài Lij của đường đi từ đỉnh i đến đỉnh j thì ta có thể lập thêm ma trận độ dài L[1..n, 1..n] như sau:
L[i, j] = Lij
3. KIỂM TRA XEM CÓ ĐƯỜNG ĐI TỪ ĐỈNH Đ ĐẾN ĐỈNH C TRÊN MỘT ĐỒ THỊ CÓ HƯỚNG HAY KHÔNG
a) Bài toán
Cho đồ thị có hướng G có ma trận nối là A và hai đỉnh Đ, C của G. Hãy tìm xem có đường đi từ Đ đến C không.
b) Thuật toán
- Dùng mảng C[1..n] of Boolean để đánh dấu các đỉnh đã đi qua.
- Dùng procedure lantu(i) một cách đệ qui để lan từ đỉnh Đ đến một đỉnh nào đó có thể được, rồi từ đó lại lan tiếp đến các đỉnh khác chưa lan tới cho đến khi gặp đỉnh thì biến Boolean kq cho kết quả true nghĩa là có đường đi.
c) Thể hiện bằng PASCAL
Procedure Lantu (i: byte);
Var j: byte;
Begin
if (i = c) then kq := True
else
Begin
For j := 1 to n do
if A[i, j] and not c[j] then
Begin
c[j] := true;
lantu (j);
end;
end;
end;
Begin {chương trình chính}
Kq := False;
For j := 1 to n do C[j] := False;
lantu (Đ);
if kq then writeln ('có đường đi');
else writeln ('không có’);
end.
4. TÌM ĐƯỜNG ĐI NGẮN NHẤT
a) Bài toán
Tìm đường đi ngắn nhất từ đỉnh nguồn (1) đến một đỉnh khác (j) của một đồ thị có hướng G có ma trận nôi là A và ma trận độ dài L chứa chiều dài các cung:
L[i, i] = 0 với mọi i = 1 ... n
L[i, j] >= 0 nếu tồn tại cung từ đỉnh i đến đỉnh j.
L[i, j] = ∞ nếu không tồn tại cung từ đỉnh i đến đỉnh j.
b) Thuật toán (Dijkstra)
- Nguyên lí chính của thuật toán này là: Nếu tồn tại đường đi ngắn nhất từ đỉnh i đến đỉnh j và đỉnh k ở trên đường đi này thì k sẽ chia đường đi thành hai đoạn và hai đoạn đó phải là hai đoạn ngắn nhất nối từ i đến k và từ k đến j.
Ta dùng hai mảng C và S.
C: chứa các đỉnh chưa được chọn.
S: chứa các đỉnh đã được chọn.
- Tại mỗi thời điểm tập S chứa các đỉnh mà khoảng cách nhỏ nhất từ đỉnh nguồn đến, chúng đã được xác định tập C chứa các đỉnh còn lại.
- Bắt đầu S = {Đỉnh nguồn}
- Kết thúc := tập các đỉnh của G.
- Tại mỗi bước ta chọn một đỉnh C mà khoảng cách D[x] từ đỉnh nguồn đến X là nhỏ nhất.
- Ta nói rằng đường đi từ đỉnh nguồn đến một đỉnh khác là đặc biệt nếu tất cả các đỉnh trung gian trên đường đi này đều ở trong tập s.
- Tại mỗi bước của thuật toán có mảng một chiều D chứa chiều dài của đường đi đặc biệt ngắn nhất đến mỗi đỉnh của đồ thị.
- Mỗi lần ta đưa đỉnh X mới vào s đường đi riêng biệt ngắn nhất đến X cũng chính là đường đi ngắn nhất trong tất cả các đường đi đến X.
- Khi thuật toán kết thúc, tất cả các đỉnh của G đều thuộc S suy ra mọi đường đi từ nguồn đến các đỉnh đều là đặc biệt.
- Ví dụ:
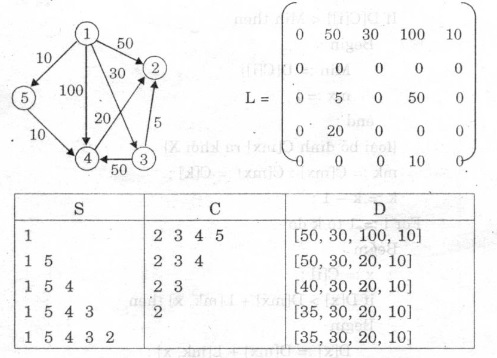 c) Thể hiện bằng PASCAL
Procedure Shortestpath;
Var D, P, C: Array[1..n] of integer;
i, j, k, mk, mx, min, x: integer;
Begin
K := n - 1: {số phần tử của C}
{Xây dựng các mảng C, D và P}
For i := 2 to n do
Begin
C[i - 1] = i;
D[i] = L[1,i];
P[i] = 1;
end;
For j :=1 to n - 2 do
Begin ({tìm giá trị nhỏ nhất của mảng D}
Min := D[C[1]]; mx := 1;
For i := 2 to k do
If D[C[i]] < Min then
Begin
Min := D[C[i]]
mx := i
end;
{loại bỏ đỉnh C[mx] ra khỏi X}
mk := C[mx]: C[mx] := C[k];
k := k - 1;
For i:= 1 to k đo
Begin
x := C[i]; .
if D[x] > D[mx] + L[mk, x] then
Begin
D[x]:= D[mx] + L[mk, xj;
P[x] mk;
end;
end;
end;
end;
Để chỉ ra đường đi ngắn nhất từ đỉnh nguồn đến đỉnh j ta có thủ tục sau:
Procedure Path (x: integer);
Begin
if x < > 1 then
Begin
Path (p[x]);
Write (x: 3); ‘.
end;
end;
Khi sử dụng ta chỉ việc gọi Path(j);
c) Thể hiện bằng PASCAL
Procedure Shortestpath;
Var D, P, C: Array[1..n] of integer;
i, j, k, mk, mx, min, x: integer;
Begin
K := n - 1: {số phần tử của C}
{Xây dựng các mảng C, D và P}
For i := 2 to n do
Begin
C[i - 1] = i;
D[i] = L[1,i];
P[i] = 1;
end;
For j :=1 to n - 2 do
Begin ({tìm giá trị nhỏ nhất của mảng D}
Min := D[C[1]]; mx := 1;
For i := 2 to k do
If D[C[i]] < Min then
Begin
Min := D[C[i]]
mx := i
end;
{loại bỏ đỉnh C[mx] ra khỏi X}
mk := C[mx]: C[mx] := C[k];
k := k - 1;
For i:= 1 to k đo
Begin
x := C[i]; .
if D[x] > D[mx] + L[mk, x] then
Begin
D[x]:= D[mx] + L[mk, xj;
P[x] mk;
end;
end;
end;
end;
Để chỉ ra đường đi ngắn nhất từ đỉnh nguồn đến đỉnh j ta có thủ tục sau:
Procedure Path (x: integer);
Begin
if x < > 1 then
Begin
Path (p[x]);
Write (x: 3); ‘.
end;
end;
Khi sử dụng ta chỉ việc gọi Path(j);
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.