Tổ hợp trong Pascal
2020-08-08T09:47:21-04:00
2020-08-08T09:47:21-04:00
https://sachgiai.com/Tin-hoc/to-hop-trong-pascal-13460.html
https://sachgiai.com/uploads/news/2020_07/lap-trinh-pascal.jpg
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Thứ bảy - 08/08/2020 09:28
Trong khi lập trình ta thường xuyên phải làm các thao tác sắp xếp, phân hoạch, lập tập con, hợp thành tập hợp lớn hơn...
1. KHÁI NIỆM
a) Trong khi lập trình ta thường xuyên phải làm các thao tác sắp xếp, phân hoạch, lập tập con, hợp thành tập hợp lớn hơn... trên một tập hợp các phần tử hữu hạn và rời rạc nghĩa là thường xuyên đụng chạm đến các khái niệm của giải tích tổ hợp, đó là:
+ Hoán vị
+ Chỉnh hợp
+ Tổ hợp
b) Hoán vị
- Một hoán vị của n phần tử là một bộ phận gồm n phần tử để được sắp xếp theo một trật tự nhất định, mỗi phần tử có mặt đúng một lần.
- Số các hoán vị khác nhau của n phần tử là:
Pn = n! = 1 x 2 x 3 x ... x n
c) Chỉnh hợp
- Một chỉnh hợp n chập r của n phần tử là một bộ sắp thứ tự gồm r phần tử lấy ra từ n phần tử đã cho.
- Số chỉnh hợp n chập r là:
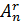 = n(n - l)...(n - r + 1)
= n(n - l)...(n - r + 1)
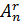 =
= 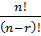 d) Tổ hợp
- Cho một tập x có n phần tử. Một tổ hợp n chập r của n phần tử đó là một tập con của X gồm có r phần tử.
- Số tổ hợp n chập r là:
d) Tổ hợp
- Cho một tập x có n phần tử. Một tổ hợp n chập r của n phần tử đó là một tập con của X gồm có r phần tử.
- Số tổ hợp n chập r là:
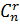 =
= 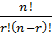
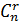 =
= 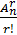 2. CÁC THUẬT TOÁN
a) Hoán vị
* Bài toán:
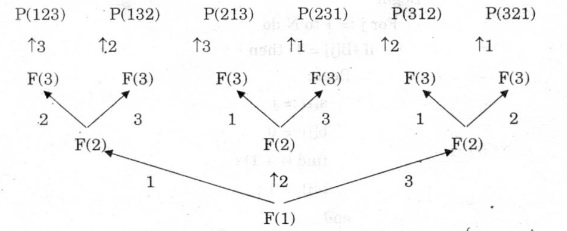
Viết chương trình in ra tất cả các hoán vị của N số tự nhiên đầu tiên.
* Thuật toán:
- Ta đặt mảng A[1..N] để chứa hoán vị tìm được.
- Mảng B[1..N] of Bollean để làm cờ với B[I] cho biết số i đã được chọn vào hoán vị hay chưa.
- Thuật toán được lập theo kiểu đệ qui với hai thủ tục là: PRINT và FIND (i: Byte).
- Thủ tục PRINT sẽ in ra hoán vị vừa tìm được.
- Thủ tục FIND (i: Byte) giúp tìm phần tử thứ i trong hoán vị và được gọi một cách đệ qui. Cơ chế hoạt động của nó như sau:
procedure FIND (i: Byte);
Var j: byte;
Begin
if i > N then Xuat
Else
Begin
For j := 1 to N do
if b[j] then
Begin
a[i] := j
b[j] := 0
Find (i + 1)
b[j] := 1;
end;
end;
end;
* Ví dụ: N = 3
2. CÁC THUẬT TOÁN
a) Hoán vị
* Bài toán:
Viết chương trình in ra tất cả các hoán vị của N số tự nhiên đầu tiên.
* Thuật toán:
- Ta đặt mảng A[1..N] để chứa hoán vị tìm được.
- Mảng B[1..N] of Bollean để làm cờ với B[I] cho biết số i đã được chọn vào hoán vị hay chưa.
- Thuật toán được lập theo kiểu đệ qui với hai thủ tục là: PRINT và FIND (i: Byte).
- Thủ tục PRINT sẽ in ra hoán vị vừa tìm được.
- Thủ tục FIND (i: Byte) giúp tìm phần tử thứ i trong hoán vị và được gọi một cách đệ qui. Cơ chế hoạt động của nó như sau:
procedure FIND (i: Byte);
Var j: byte;
Begin
if i > N then Xuat
Else
Begin
For j := 1 to N do
if b[j] then
Begin
a[i] := j
b[j] := 0
Find (i + 1)
b[j] := 1;
end;
end;
end;
* Ví dụ: N = 3
 * Thể hiện bằng PASCAL:
PROGRAM HOANVI;
Const N = 3;
Var
A: Array [1..N] of byte;
B: Array [1..N] of 0..1;
i, dem: integer;
Procedure xuat;
var i: integer;
Begin
dem := dem + 1;
write (’Hoan vi thu', dem, ’ ');
For i:= 1 to N do write (A[i]);
Writein ;
readln ;
end;
Procedure Find (i: byte);
var j: byte;
Begin
if i > N then Xuat
else
Begin
For j := 1 to N do
if (B[j] = 1) then
Begin
a[i] := j;
b[j] := 0;
find (i + 1);
b[j] := 1;
end;
end;
end;
BEGIN
dem := 0;
For i: 1 to N do B[i]:= 1;
Find(l);
END.
b) Chỉnh hợp
* Bài toán:
Viết chương trình in ra tất cả các chỉnh hợp n chập r của số tự nhiên đầu tiên (r ≤ n).
* Thuật toán:
- Tương tự như phần hoán vị.
- Chỉ cần sửa thủ tục Find(i) lại như sau:
Procedure Find (i: byte);
var j: byte
Begin
if i > r then xuat
else...
* Ví dụ:
N = 3, r = 2
* Thể hiện bằng PASCAL:
PROGRAM HOANVI;
Const N = 3;
Var
A: Array [1..N] of byte;
B: Array [1..N] of 0..1;
i, dem: integer;
Procedure xuat;
var i: integer;
Begin
dem := dem + 1;
write (’Hoan vi thu', dem, ’ ');
For i:= 1 to N do write (A[i]);
Writein ;
readln ;
end;
Procedure Find (i: byte);
var j: byte;
Begin
if i > N then Xuat
else
Begin
For j := 1 to N do
if (B[j] = 1) then
Begin
a[i] := j;
b[j] := 0;
find (i + 1);
b[j] := 1;
end;
end;
end;
BEGIN
dem := 0;
For i: 1 to N do B[i]:= 1;
Find(l);
END.
b) Chỉnh hợp
* Bài toán:
Viết chương trình in ra tất cả các chỉnh hợp n chập r của số tự nhiên đầu tiên (r ≤ n).
* Thuật toán:
- Tương tự như phần hoán vị.
- Chỉ cần sửa thủ tục Find(i) lại như sau:
Procedure Find (i: byte);
var j: byte
Begin
if i > r then xuat
else...
* Ví dụ:
N = 3, r = 2
 * Thể hiện bằng PASCAL:
PROGRAM CHINHHOP;
Var
A: Array [1..N] of byte;
B: Array [1..N] of 0..1;
i, j, dem: byte;
Procedure Xuat;
Var
i: byte;
Begin
dem := dem + 1;
write (’Hoan vi thu dem, ':;
For i: = 1 to r do write (A[i]);
writein;
Readln;
end;
Procedure Find (i: byte);
Var j: byte;
Begin
if i > r -then Xuat
else
For j:= 1 to n do
if (B[j] = 1) then
Begin
A[i] := j;
B[j] := 0;
Find (i + 1);
B[j] := 1;
end;
end;
BEGIN
writeiln (‘Nhập r');
Readln(r);
Dem:= 0;
For i : 1 to b do B[i] := 1;
Find(l);
END.
c) Tổ hợp
* Bài toán:
Viết chương trình in ra màn hình tất cả các tổ hợp n chập r của các số nguyên từ 1 đến n.
* Thuật toán:
• THUẬT TOÁN 1:
- Tương tự như thuật toán tìm các chỉnh hợp n chập r nhưng ở đây ta chỉ cần chọn 1 chỉnh hợp có thứ tự tăng.
- Thủ tục Find được cải tiến như sau:
Procedure Find (k: byte);
Var
j: byte;
Begin
if k > r then xuat
else
Begin
For j := 1 to n do
if b[j] and (j > a[k – 1]) then
begin
a[k] := j; .
b[j]:= False;
Find [k + 1];
b[i] := True;
end;
end;
End;
• THUẬT TOÁN 2.
- Do trong tổ hợp ta chỉ cần tìm từ nhỏ đến lớn và không cần quay lại nên ta có thể không cần tìm i đặt cờ B[1..N] of Boolean.
- Thủ tục Find (i: byte) có thể viết như sau:
Procedure Find (i: byte)
Var
i: byte;
Begin
If k > r then xuat
Else
For i:= (A[k - 1] + 1) to n do
Begin
B[K] := i
Find (k + 1);
end;
end;
• THUẬT TOÁN:
- Chỉ cần đặt các cờ A[1..N] of 0..1
- Lần lượt cho các A[i] bằng 1 hoặc 0
A[i]:= 1: số i được chọn vào tổ hợp.
A[i]:= 0: số i không được chọn vào tổ hợp.
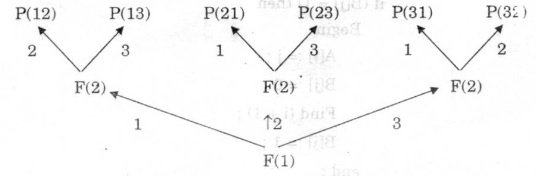
■ Ví dụ: N = 3, r = 2
Giải thuật của ta chạy hết cây chọn lựa sau đây để tìm ra tất cả các tổ hợp 3 chập 2 của tập X = (1, 2, 3);
* Thể hiện bằng PASCAL:
PROGRAM CHINHHOP;
Var
A: Array [1..N] of byte;
B: Array [1..N] of 0..1;
i, j, dem: byte;
Procedure Xuat;
Var
i: byte;
Begin
dem := dem + 1;
write (’Hoan vi thu dem, ':;
For i: = 1 to r do write (A[i]);
writein;
Readln;
end;
Procedure Find (i: byte);
Var j: byte;
Begin
if i > r -then Xuat
else
For j:= 1 to n do
if (B[j] = 1) then
Begin
A[i] := j;
B[j] := 0;
Find (i + 1);
B[j] := 1;
end;
end;
BEGIN
writeiln (‘Nhập r');
Readln(r);
Dem:= 0;
For i : 1 to b do B[i] := 1;
Find(l);
END.
c) Tổ hợp
* Bài toán:
Viết chương trình in ra màn hình tất cả các tổ hợp n chập r của các số nguyên từ 1 đến n.
* Thuật toán:
• THUẬT TOÁN 1:
- Tương tự như thuật toán tìm các chỉnh hợp n chập r nhưng ở đây ta chỉ cần chọn 1 chỉnh hợp có thứ tự tăng.
- Thủ tục Find được cải tiến như sau:
Procedure Find (k: byte);
Var
j: byte;
Begin
if k > r then xuat
else
Begin
For j := 1 to n do
if b[j] and (j > a[k – 1]) then
begin
a[k] := j; .
b[j]:= False;
Find [k + 1];
b[i] := True;
end;
end;
End;
• THUẬT TOÁN 2.
- Do trong tổ hợp ta chỉ cần tìm từ nhỏ đến lớn và không cần quay lại nên ta có thể không cần tìm i đặt cờ B[1..N] of Boolean.
- Thủ tục Find (i: byte) có thể viết như sau:
Procedure Find (i: byte)
Var
i: byte;
Begin
If k > r then xuat
Else
For i:= (A[k - 1] + 1) to n do
Begin
B[K] := i
Find (k + 1);
end;
end;
• THUẬT TOÁN:
- Chỉ cần đặt các cờ A[1..N] of 0..1
- Lần lượt cho các A[i] bằng 1 hoặc 0
A[i]:= 1: số i được chọn vào tổ hợp.
A[i]:= 0: số i không được chọn vào tổ hợp.
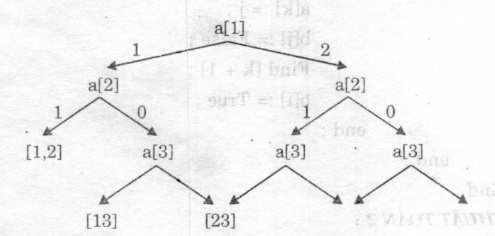
■ Ví dụ: N = 3, r = 2
Giải thuật của ta chạy hết cây chọn lựa sau đây để tìm ra tất cả các tổ hợp 3 chập 2 của tập X = (1, 2, 3);
 Thủ tục Find được viết lại như sau:
procedure Find (i: byte);
Var j: byte;
Begin
if d > r then print
Else
if ((n + 1 - i) > (r - d)) then
Begin
For j := 1 down to 0 do
A[i] := j;
d := d + j;
Find (i + 1);
d :=d - j;
A[i] := A[i] - j;
end;
end;
* Thể hiện bằng PASCAL:
PROGRAM TOHOP1;
Const n = 10
Var A: array [0..N] of byte;
B: array [1..N] of Boolean;
r, dem, t: integer;
procedure print;
var i: byte;
Begin
Dem:= dem + 1;
Write ('to hop thu', dem, 'la :');
For i := 1 to r do write (a[i]);
writeln;
readln;
end;
{……………………………….}
Procedure Find (k: byte);
Var j: byte;
Begin
if k > r then print
else
Begin
For j:= 1 to n do
if b[j] and (j > a[k - 1]) then
Begin
a[k] := j;
b[j] := False.;
Find [k + 1];
b[j] := True;
end;
end;
end;
BEGIN
write ('Cho biet so phan tu:’);
Readin (r);
dem := 0;
For t: = 1 to n do b[t]:= true
a[0] := 0;
Find(l);
END.
{………………………….}
PROGRAM TOHOP2;
const N = 10;
Var A: array [0..N] of byte;
dem, r: byte;
{……………………..}
procedure print;
Var i: byte;
Begin
Dem := dem + 1;
For i: = 1 to r do write (A[i]);
Writein;
Readin;
end;
{………………………….}
Procedure Find (j = byte);
Var i: byte;
Begin
if j > r then print
else
For i:= A[j - 1] to n do
Begin
B[j] := i ;
Find(j + 1);
end;
End;
BEGIN
Dem := 0;
a[0] := 0;
Readln(r);
Find(1);
END.
{………………………….}
PROGRAM TOHOP3;
Var A: array [0..n] of 0..1;
r, d : byte;
procedure Print;
Var i: byte;
Begin
d := d + 1;
write ('To hop thu', d, '{');
For i := 1 to n do
if A[i] := 1 then write (i);
Write(‘{');
Writeln;
Readln;
end;
{………………………….}
Procedure Find (i = byte);
Var j: byte;
Begin
if d > r then print
Else
if (n + 1 - i) > (r - d) then
For j := down to 0 do
Begin
A[i] := j;
d := d + j
Find(i + 1)
d := d - j;
end;
End;
BEGIN
d := 0;
writeln ('Nhap r');
Readln(r);
Fill char (A, size of (A); 0);
Find(l);
END.
Thủ tục Find được viết lại như sau:
procedure Find (i: byte);
Var j: byte;
Begin
if d > r then print
Else
if ((n + 1 - i) > (r - d)) then
Begin
For j := 1 down to 0 do
A[i] := j;
d := d + j;
Find (i + 1);
d :=d - j;
A[i] := A[i] - j;
end;
end;
* Thể hiện bằng PASCAL:
PROGRAM TOHOP1;
Const n = 10
Var A: array [0..N] of byte;
B: array [1..N] of Boolean;
r, dem, t: integer;
procedure print;
var i: byte;
Begin
Dem:= dem + 1;
Write ('to hop thu', dem, 'la :');
For i := 1 to r do write (a[i]);
writeln;
readln;
end;
{……………………………….}
Procedure Find (k: byte);
Var j: byte;
Begin
if k > r then print
else
Begin
For j:= 1 to n do
if b[j] and (j > a[k - 1]) then
Begin
a[k] := j;
b[j] := False.;
Find [k + 1];
b[j] := True;
end;
end;
end;
BEGIN
write ('Cho biet so phan tu:’);
Readin (r);
dem := 0;
For t: = 1 to n do b[t]:= true
a[0] := 0;
Find(l);
END.
{………………………….}
PROGRAM TOHOP2;
const N = 10;
Var A: array [0..N] of byte;
dem, r: byte;
{……………………..}
procedure print;
Var i: byte;
Begin
Dem := dem + 1;
For i: = 1 to r do write (A[i]);
Writein;
Readin;
end;
{………………………….}
Procedure Find (j = byte);
Var i: byte;
Begin
if j > r then print
else
For i:= A[j - 1] to n do
Begin
B[j] := i ;
Find(j + 1);
end;
End;
BEGIN
Dem := 0;
a[0] := 0;
Readln(r);
Find(1);
END.
{………………………….}
PROGRAM TOHOP3;
Var A: array [0..n] of 0..1;
r, d : byte;
procedure Print;
Var i: byte;
Begin
d := d + 1;
write ('To hop thu', d, '{');
For i := 1 to n do
if A[i] := 1 then write (i);
Write(‘{');
Writeln;
Readln;
end;
{………………………….}
Procedure Find (i = byte);
Var j: byte;
Begin
if d > r then print
Else
if (n + 1 - i) > (r - d) then
For j := down to 0 do
Begin
A[i] := j;
d := d + j
Find(i + 1)
d := d - j;
end;
End;
BEGIN
d := 0;
writeln ('Nhap r');
Readln(r);
Fill char (A, size of (A); 0);
Find(l);
END.
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.