Quy hoạch động trong Pascal
2020-08-10T11:44:38-04:00
2020-08-10T11:44:38-04:00
https://sachgiai.com/Tin-hoc/quy-hoach-dong-trong-pascal-13468.html
https://sachgiai.com/uploads/news/2020_07/lap-trinh-pascal.jpg
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Thứ hai - 10/08/2020 11:41
Nguyên lí “chia để trị” thường đóng vai trò chủ đạo trong việc thiết kế thuật toán: để giải quyết một bài toán lớn, chúng ta chia nó thành nhiều bài toán con có thể giải quyết được độc lập
1. Nguyên lí tối ưu của Bellman
- Trong một dãy tối ưu các lựa chọn thì mọi dây con của nó cũng tối im.
- Điều kiện tối ưu không phụ thuộc vào tiền sử của hệ điều khiển mà chỉ phụ thuộc vào trạng thái tức thời và mục tiêu cuối cùng của hệ điều khiển.
2. Kĩ thuật của qui hoạch động
- Lập chương trình qui hoạch động.
- Lập bảng lưu lại các nghiệm của bài toán con.
3. Triết lí của qui hoạch động
- Nguyên lí “chia để trị” thường đóng vai trò chủ đạo trong việc thiết kế thuật toán: để giải quyết một bài toán lớn, chúng ta chia nó thành nhiều bài toán con có thể giải quyết được độc lập.
- Trong phương pháp qui hoạch động, việc thể hiện nguyên lí này được đẩy đến cực độ.
• Khi không biết chắc cần giải quyết bài toán con nào chúng ta , giải quyết tất cả các bài toán con và lưu trữ những lời giải này với mục đích sử dụng lại chúng theo một sự phôi hợp nào đó để giải quyết các bài toán tổng quát hơn.
4. Hạn chế của phương pháp qui hoạch động
- Không phải lúc nào sự kết hợp lời giải của các bài toán con cũng cho ta lời giải của bài toán lớn hơn.
- Số lượng các bài toán con cần giải quyết và lưu trữ đáp án có thể rất lớn, không thể chấp nhận được.
■ Ví dụ 1:
Cho n đồ vật, đồ vật thứ i có thể tích là V[i] và có giá trị là p[i]. Cần phải quyết định xem nên xếp những vật nào trong n vật trên vào trong một ba lô có thể tích V sao cho tổng giá trị của đồ vật được xếp vào ba lô là cực đại.
Giải
Ta phải tìm [L1 L2, L3, Ln] với L1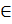 {0,1} thỏa:
ΣLiVi ≤ V
và ΣLiPi đạt Max.
Đặt M[i,j] là giá trị lớn nhất đạt được của ba lô khi xét đến vật thứ i có thể tích còn lại là j.
Ta có phương trình qui hoạch động:
M[i,j] = Max{M[i-1,j-V[i]] + P[i] ;M[i-1,j])
Chương trình PASCAL đầy đủ như sau:
Program balo:
uses crt;
Const
MaxVat=50 ;
MaxKt=100 ;
Var M: Array[0..MaxVat,0..MaxKt] of word;
v,p: Array[1..MaxVat] of byte;
Lap: Array[l..MaxVat] of boolean;
so vat, kt: byte;
Procedure Nhap;
var i: byte;
Begin
clrscr;
Writeln(‘CHUONG TRINH XEP BALO') ;
Writeln(‘…………………………………’);
fillchar(p,sizeof(p),0);
fillchar(p,sizeof(v),0);
Write(Nhap so do vat can xep [1..'<MaxVat,'] : ') ;
Readln(sovat);
Write(‘Nhap the tich balo [1..',MaxKt,’] : ').;readln(Kt);
For i: = 1 to sovat do
Begin
Write(‘Nhap vat thu',i,'[V-$] : ');
readln(v[i],p[i]) ;
End;
Writeln(‘Solving...’);delay(100);
End;
Function GetMax(a,b: word) : Word;
Begin
if a > b then GetMax : = a else GetMax: = b;
end;
Procedure Taobang;
var i,j : byte;
Begin
Fillchar(M,Sizeof(m),0) ;
fillchar(lay,sizeof(lay),false);
For i : = 1 to sovat do
For j : = kt down to 1 do
Begin
If j - V[i] >= 0 then M[i,j] : = GetMax(M[i-1,j-v[i]] + p[i],
M[i-1,j])
Else M[i,j] : = M[i-1,j];
End;
End;
Procedure InBang;
var i,j : byte;
Begin
for i: = 0 to sovat do
Begin
for j : = 0 to Kt do
Write(M[i,j] : 3);
Writeln;
end;
end;
Procedure TruyHoi;
Var i,1 : byte;
max : word;
Begin
Max : = 0;
for i : = 1 to Kt do
If Max <- M[sovat,i] then
Begin
Max : = M[sovat,i] ;1: = i
end;
For i : = sovat down to 1 do
Begin
If M[i,1] < > M[i-1,1] then
Begin
Lay [i] : = true;
1 : = 1-V[i];
End;
End;
writeln;
write!('Lay cac vat :’) ;
For i : = 1 to sovat do
If lay[i] then write(i: 3);
Write(‘Gia tri tong cong: ’,Max);
readln;
end;
Begin
Nhap;
Taobang;
{InBang;}
Truyhoi;
end.
■ Ví dụ 2: Cho G = (V,E) là đồ thị có hướng. V là tập đỉnh. E là tập cạnh. Mỗi cạnh có độ dài dương, cần tìm đường đi ngắn nhất nối mỗi cặp đỉnh.
Giải
Theo nguyên lí tối ưu của qui hoạch động:
Nếu đường đi ngắn nhất từ i đến j có đi qua k thì phần của đường đi đó từ i đến k và từ k đến j cũng phải ngắn nhất.
Đặt A[i,j] là độ dài đường đi ngắn nhất từ i đến j. Ta xây dựng A như sau:
- Lúc đầu A: = D;
- Sau đó lặp n lần, sau lần lặp thứ k, A sẽ cho độ dài các đường đi ngắn nhất trong các đỉnh |1,2,...,k]. Ta có phương trình qui hoạch động để tính A ở bước k:
Ak[i,j] = Min {Ak-1[i,j], Ak-1[i,k] + Ak-1[k,j]}
Chương trình PASCAL đầy đủ như sau:
uses crt;
const maxn = 100;
var a: array[1..maxn,1..maxn] of word;
c: array[1..maxn,1..maxn] of byte;
dinh dau,dinh cuoi: byte;
n: byte;
found: boolean;
m: byte;
d: word;
procedure floydbellman;
var i,j,k : byte;
begin
for k: = 1 to n do
for i: = 1 to n do
for j: = 1 to n do
if (a[i,k]+a[k,j]<a[i,j]) then
begin
a[i,j] : = a[i,k]+a[k,j]
a[i,j] : = a[i,j];
c[i,j] : = k;
c[j,i]: = c[i,j];
end;
end;
Procedure find(i j : byte);
begin
if (c[i,j] = 0) then
begin
if a[i,j] = maxint then found : = false
esle if moi then write(i: 2,'->');
end;
else
begin
Find(i,c[i,j]) ;
Find(c[i,j],j) ;
Write(j : 2,'->’)
M : = j;
end;
Procedure Nhap;
var i,j : byte;
d: word;
f: text;
Begin
Assign(f,'d: \tp5\Fb.inp');
Reset(f);
Readln(f,n);
For i : = 1 to n do
Begin
For j : = 1 to n do
Read(f,n);
If d< >0 then A[i,j] : = d;
Readln(f);
End;
Closet (f);
End;
Procedure Xuat;
Begin
Repeat
Writeln;
Write(‘Nhap dinh dau :');
Readln(dinh_dau);
Write(‘Nhap dinh cuoi :’);
Readln(dinh_cuoi);
found : = true;
m : = maxn+1;
fin(dinh_dau,dinh_cuoi);
if not found then writeln(‘khong co duong di tu',dinh_dau,'den',dinh_cuoi,'.')
else
begin
GotoXY(Where-2,Wherey);
Writeln(‘ ')
end;
Write(‘tiep tuc (C/K) ?');
Until Upcase (readkey) < > 'c';
end;
Procedure Khoitao;
var i,j: byte;
begin
For i : = 1 to maxn do
For j : = 1 to maxn do a[i,j] : = maxint
For i : = 1 to maxn do a[i,i] : = 0;
FillChar(c,Sizeof(c),0);
end;
BEGIN
khoitao;
Nhap;
Floydbellman;
Xuat;
END.
{0,1} thỏa:
ΣLiVi ≤ V
và ΣLiPi đạt Max.
Đặt M[i,j] là giá trị lớn nhất đạt được của ba lô khi xét đến vật thứ i có thể tích còn lại là j.
Ta có phương trình qui hoạch động:
M[i,j] = Max{M[i-1,j-V[i]] + P[i] ;M[i-1,j])
Chương trình PASCAL đầy đủ như sau:
Program balo:
uses crt;
Const
MaxVat=50 ;
MaxKt=100 ;
Var M: Array[0..MaxVat,0..MaxKt] of word;
v,p: Array[1..MaxVat] of byte;
Lap: Array[l..MaxVat] of boolean;
so vat, kt: byte;
Procedure Nhap;
var i: byte;
Begin
clrscr;
Writeln(‘CHUONG TRINH XEP BALO') ;
Writeln(‘…………………………………’);
fillchar(p,sizeof(p),0);
fillchar(p,sizeof(v),0);
Write(Nhap so do vat can xep [1..'<MaxVat,'] : ') ;
Readln(sovat);
Write(‘Nhap the tich balo [1..',MaxKt,’] : ').;readln(Kt);
For i: = 1 to sovat do
Begin
Write(‘Nhap vat thu',i,'[V-$] : ');
readln(v[i],p[i]) ;
End;
Writeln(‘Solving...’);delay(100);
End;
Function GetMax(a,b: word) : Word;
Begin
if a > b then GetMax : = a else GetMax: = b;
end;
Procedure Taobang;
var i,j : byte;
Begin
Fillchar(M,Sizeof(m),0) ;
fillchar(lay,sizeof(lay),false);
For i : = 1 to sovat do
For j : = kt down to 1 do
Begin
If j - V[i] >= 0 then M[i,j] : = GetMax(M[i-1,j-v[i]] + p[i],
M[i-1,j])
Else M[i,j] : = M[i-1,j];
End;
End;
Procedure InBang;
var i,j : byte;
Begin
for i: = 0 to sovat do
Begin
for j : = 0 to Kt do
Write(M[i,j] : 3);
Writeln;
end;
end;
Procedure TruyHoi;
Var i,1 : byte;
max : word;
Begin
Max : = 0;
for i : = 1 to Kt do
If Max <- M[sovat,i] then
Begin
Max : = M[sovat,i] ;1: = i
end;
For i : = sovat down to 1 do
Begin
If M[i,1] < > M[i-1,1] then
Begin
Lay [i] : = true;
1 : = 1-V[i];
End;
End;
writeln;
write!('Lay cac vat :’) ;
For i : = 1 to sovat do
If lay[i] then write(i: 3);
Write(‘Gia tri tong cong: ’,Max);
readln;
end;
Begin
Nhap;
Taobang;
{InBang;}
Truyhoi;
end.
■ Ví dụ 2: Cho G = (V,E) là đồ thị có hướng. V là tập đỉnh. E là tập cạnh. Mỗi cạnh có độ dài dương, cần tìm đường đi ngắn nhất nối mỗi cặp đỉnh.
Giải
Theo nguyên lí tối ưu của qui hoạch động:
Nếu đường đi ngắn nhất từ i đến j có đi qua k thì phần của đường đi đó từ i đến k và từ k đến j cũng phải ngắn nhất.
Đặt A[i,j] là độ dài đường đi ngắn nhất từ i đến j. Ta xây dựng A như sau:
- Lúc đầu A: = D;
- Sau đó lặp n lần, sau lần lặp thứ k, A sẽ cho độ dài các đường đi ngắn nhất trong các đỉnh |1,2,...,k]. Ta có phương trình qui hoạch động để tính A ở bước k:
Ak[i,j] = Min {Ak-1[i,j], Ak-1[i,k] + Ak-1[k,j]}
Chương trình PASCAL đầy đủ như sau:
uses crt;
const maxn = 100;
var a: array[1..maxn,1..maxn] of word;
c: array[1..maxn,1..maxn] of byte;
dinh dau,dinh cuoi: byte;
n: byte;
found: boolean;
m: byte;
d: word;
procedure floydbellman;
var i,j,k : byte;
begin
for k: = 1 to n do
for i: = 1 to n do
for j: = 1 to n do
if (a[i,k]+a[k,j]<a[i,j]) then
begin
a[i,j] : = a[i,k]+a[k,j]
a[i,j] : = a[i,j];
c[i,j] : = k;
c[j,i]: = c[i,j];
end;
end;
Procedure find(i j : byte);
begin
if (c[i,j] = 0) then
begin
if a[i,j] = maxint then found : = false
esle if moi then write(i: 2,'->');
end;
else
begin
Find(i,c[i,j]) ;
Find(c[i,j],j) ;
Write(j : 2,'->’)
M : = j;
end;
Procedure Nhap;
var i,j : byte;
d: word;
f: text;
Begin
Assign(f,'d: \tp5\Fb.inp');
Reset(f);
Readln(f,n);
For i : = 1 to n do
Begin
For j : = 1 to n do
Read(f,n);
If d< >0 then A[i,j] : = d;
Readln(f);
End;
Closet (f);
End;
Procedure Xuat;
Begin
Repeat
Writeln;
Write(‘Nhap dinh dau :');
Readln(dinh_dau);
Write(‘Nhap dinh cuoi :’);
Readln(dinh_cuoi);
found : = true;
m : = maxn+1;
fin(dinh_dau,dinh_cuoi);
if not found then writeln(‘khong co duong di tu',dinh_dau,'den',dinh_cuoi,'.')
else
begin
GotoXY(Where-2,Wherey);
Writeln(‘ ')
end;
Write(‘tiep tuc (C/K) ?');
Until Upcase (readkey) < > 'c';
end;
Procedure Khoitao;
var i,j: byte;
begin
For i : = 1 to maxn do
For j : = 1 to maxn do a[i,j] : = maxint
For i : = 1 to maxn do a[i,i] : = 0;
FillChar(c,Sizeof(c),0);
end;
BEGIN
khoitao;
Nhap;
Floydbellman;
Xuat;
END.
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.