Giải vở bài tập Toán Hình học 7 chương II bài 3: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
2019-10-28T23:15:15-04:00
2019-10-28T23:15:15-04:00
https://sachgiai.com/Toan-hoc/giai-vo-bai-tap-toan-hinh-hoc-7-chuong-ii-bai-3-truong-hop-bang-nhau-thu-nhat-cua-tam-giac-canh-canh-canh-c-c-c-12641.html
/themes/whitebook/images/no_image.gif
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Thứ hai - 28/10/2019 23:15
Hướng dẫn Giải vở bài tập Toán Hình học 7 chương II bài 3: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c) - Luyện tập
Bài 1.
Vẽ đoạn thẳng MP = 5cm.
Trên cùng một nửa mặt phẳng bờ MP vẽ cung tròn tâm M bán kính 2,5cm và cung tròn tâm P bán kính 3cm.
Gọi giao điểm của hai cung tròn tâm M và tâm P là điểm N. Vẽ các đoạn thẳng MN, NP, ta được MN = 2,5cm, NP = 3cm.
Bài 2.
Vẽ đoạn thẳng BC = 3cm.
Trên cùng nửa mặt phẳng bờ BC vẽ cung tròn tâm B, tâm C có cùng bán kính là 3cm.
Gọi giao điểm của hai cung tròn tâm B và tâm C là điểm A.
Vẽ các đoạn thẳng AB, AC ta được Δ ABC đều.
Dùng thước đo góc đo các góc của tam giác ABC, ta được 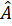 =
= 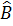 =
= 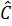 = 60°.
Bài 3.
= 60°.
Bài 3.
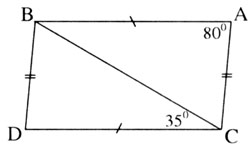 Xét Δ ABC và Δ DCB, ta có:
AB = DC (gt)
Cạnh BC chung.
AC = BD (gt)
Vậy ΔABC= ΔDCB (c.c.c).
Suy ra
Xét Δ ABC và Δ DCB, ta có:
AB = DC (gt)
Cạnh BC chung.
AC = BD (gt)
Vậy ΔABC= ΔDCB (c.c.c).
Suy ra 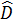 =
= 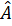 = 80°,
= 80°,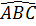 =
= 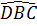 = 35°
Xét ΔABC, ta có
= 35°
Xét ΔABC, ta có 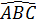 = 180° -
= 180° - 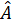 -
- 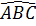 = 180° - 80° - 35° = 65°.
Xét A DCB, ta có
= 180° - 80° - 35° = 65°.
Xét A DCB, ta có 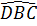 = 180° -
= 180° - 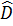 -
- 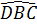 = 180° - 80° - 35° = 65°.
LUYỆN TẬP 1
= 180° - 80° - 35° = 65°.
LUYỆN TẬP 1
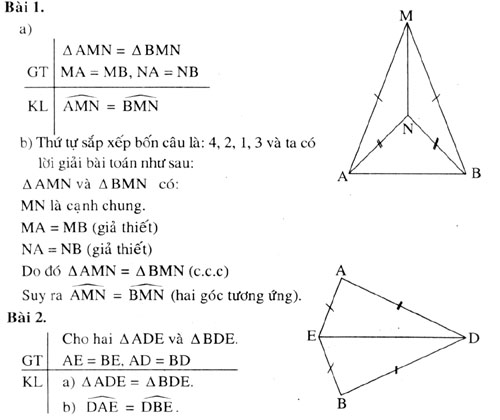 a) Xét ΔADE và ΔBDE, có:
Cạnh ED chung.
AE = BE (giả thiết)
AD = BD (giả thiết)
Vậy Δ ADE = Δ BDE(c.c.c).
b) Δ ADE = Δ BDE (theo câu a).
Suy ra
a) Xét ΔADE và ΔBDE, có:
Cạnh ED chung.
AE = BE (giả thiết)
AD = BD (giả thiết)
Vậy Δ ADE = Δ BDE(c.c.c).
b) Δ ADE = Δ BDE (theo câu a).
Suy ra 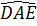 =
=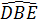 (hai góc tương ứng).
Bài 3:
(hai góc tương ứng).
Bài 3:
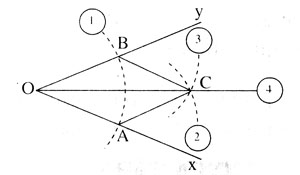 Nối A với C và B với C. Δ OAC và Δ OBC có:
Cạnh OC chung.
OA = OB (cùng bằng bán kính cung tròn tâm O).
AC = BC (hai cung tròn có cùng bán kính).
Vậy Δ OAC= Δ OBC (c.c.c).
Suy ra
Nối A với C và B với C. Δ OAC và Δ OBC có:
Cạnh OC chung.
OA = OB (cùng bằng bán kính cung tròn tâm O).
AC = BC (hai cung tròn có cùng bán kính).
Vậy Δ OAC= Δ OBC (c.c.c).
Suy ra 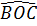 =
= 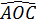 (hai góc tương ứng).
Mà tia OC nằm trong
(hai góc tương ứng).
Mà tia OC nằm trong 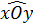 , do đó tia OC là tia phân giác của
, do đó tia OC là tia phân giác của 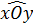 .
Bài 4.
.
Bài 4.
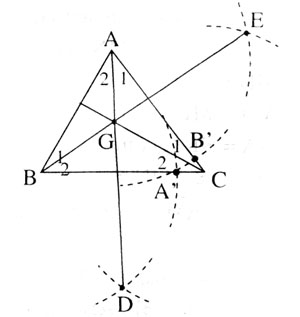 * Vẽ tia phân giác của góc A.
Dùng compa vẽ cung tròn tâm A, bán kính AB, cắt AC tại B'
Vẽ hai cung tròn tâm B và B', bán kính AB; chúng cắt nhau tại D.
AD là tia phân giác của
* Vẽ tia phân giác của góc A.
Dùng compa vẽ cung tròn tâm A, bán kính AB, cắt AC tại B'
Vẽ hai cung tròn tâm B và B', bán kính AB; chúng cắt nhau tại D.
AD là tia phân giác của 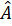 .
* Phân giác của B và C vẽ tương tự như phân giác của góc A.
Dùng compa vẽ cung tròn tâm B, bán kính AB, cắt BC tại A'.
Vẽ hai cung tròn tâm A và A’, bán kính AB; chúng cắt nhau tại E
BE là tia phân của góc
.
* Phân giác của B và C vẽ tương tự như phân giác của góc A.
Dùng compa vẽ cung tròn tâm B, bán kính AB, cắt BC tại A'.
Vẽ hai cung tròn tâm A và A’, bán kính AB; chúng cắt nhau tại E
BE là tia phân của góc 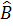 và cắt AD tại G.
Nối CG ta được tia phân giác của góc
và cắt AD tại G.
Nối CG ta được tia phân giác của góc 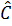 .
Vậy AD, BE, CG lần lượt là các tia phân giác của góc
.
Vậy AD, BE, CG lần lượt là các tia phân giác của góc 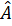 ,
, 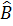 và
và 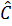 .
LUYỆN TẬP 2
Bài 1.
.
LUYỆN TẬP 2
Bài 1.
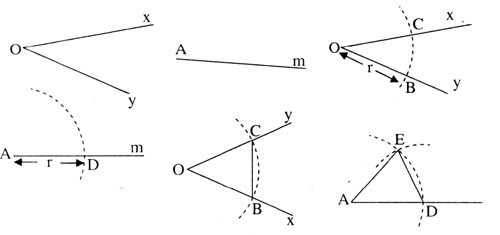 Xét Δ ADE và Δ OBC ta có:
AD = OB = r (theo cách vẽ)
AE = OC = r (vì C ∈ (O; r) và E 6 (O; r) (theo cách vẽ)).
DE = BC (theo cách vẽ).
Vậy Δ ADE= Δ OBC (c.c.c). Suy ra
Xét Δ ADE và Δ OBC ta có:
AD = OB = r (theo cách vẽ)
AE = OC = r (vì C ∈ (O; r) và E 6 (O; r) (theo cách vẽ)).
DE = BC (theo cách vẽ).
Vậy Δ ADE= Δ OBC (c.c.c). Suy ra 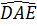 =
= 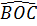 , hay
, hay 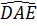 =
= 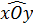 .
Bài 2.
.
Bài 2.
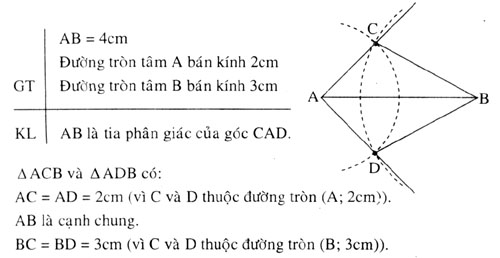 Vậy Δ ACB = Δ ADB (c.c.c), suy ra
Vậy Δ ACB = Δ ADB (c.c.c), suy ra 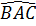 =
= 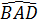 , do đó AB là tia phân giác của góc CAD.
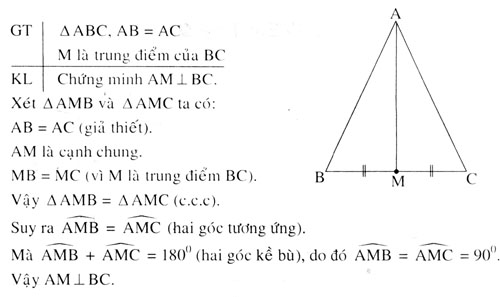
Bài 3.
, do đó AB là tia phân giác của góc CAD.
Bài 3.
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.