Ôn tập hè Toán 6 bài 1: Các phép tính trong tập hợp các số tự nhiên
2020-07-13T10:36:39-04:00
2020-07-13T10:36:39-04:00
https://sachgiai.com/Toan-hoc/on-tap-he-toan-6-bai-1-cac-phep-tinh-trong-tap-hop-cac-so-tu-nhien-13388.html
/themes/whitebook/images/no_image.gif
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Thứ hai - 13/07/2020 10:26
Ôn tập hè Toán 6 bài 1: Các phép tính trong tập hợp các số tự nhiên
A. Kiến thức cơ bản
1. Phép cộng và phép nhân
• Phép cộng và phép nhân đều có các tính chất giao hoán và kết hợp :
- Giao hoán :a + b = b + a; a . b = b . a;
- Kết hợp: (a + b) + c = a + (b + c); (a . b). c = a . (b . c).
• Nếu a. b = 0 thì có ít nhất một trong hai thừa số a hoặc b bằng 0.
• Giữa phép nhân và phép cộng có tính chất phân phối:
a . (b + c) = ab + ac.
2. Phép trừ và phép chia
• Phép trừ: a - b = x
(số bị trừ) (số trừ) (hiệu)
Điểu kiện để thực hiên được phép trừ là a > b.
• Phép chia hết và phép chia có dư:
a = b . q + r
(số bị chia) (số chia) (thương) (số dư)
Số chia bao giờ cũng khác 0 (b ≠ 0).
Số dư bao giờ cũng nhỏ hơn số chia (r < b).
Nếu r = 0 ta được phép chia hết (a = b . q).
Nếu r # 0 ta được phép chia có dư (a = b . q + r, 0 < r < b).
3. Lũy thừa với số mũ tự nhiên
• Khi nhân hai luỹ thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
am . an = am+n
• Khi chia hai luỹ thừa cùng cơ số khác 0, ta giữ nguyên cơ số và trừ các số mũ.
am : an = am-n (a ≠ 0 và m ≥ n).
Ta quy ước : a° = I ( a ≠ 0).
4. Thứ tự thực hiện các phép tính
• Trường hợp biểu thức không có dấu ngoặc :
- Nếu chỉ có phép cộng, trừ hoặc chỉ có phép nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.
- Nếu có các phép tính cộng, trừ, nhân chia, nâng lên luỹ thừa, ta thực hiện phép nâng lên luỹ thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
• Trường hợp biểu thức có dấu ngoặc
Ta thực hiện phép tính trong ngoặc tròn ( ) trước rồi thực hiện phép tính trong dấu ngoặc vuông [ ], cuối cùng thực hiện phép tính trong dấu ngoặc nhọn { }.
Sơ đồ vẻ thứ tự thực hiện các phép tính
 B. MỘT SỐ VÍ DỤ
Ví dụ 1. Tìm số tự nhiên x, biết:
a) x < 3 ;
b) 2 < x ≤ 5;
c) x là số chẵn sao cho 12 < x < 20;
d) x ∉ ℕ*
Giải.
a) x ∈ N và x < 3 nên x ∈ {0; 1 ;2}.
b) x ∈ N và 2 < x ≤ 5 nên x ∈ {3 ; 4 ; 5}.
c) x là số chẵn và 12 ≤ x < 20 nên x ∈ {12 ; 14 ; 16 ; 18}.
d) x ∈ ℕ và x ∉ ℕ* nên x = 0.
Ví dụ 2. Tìm các số tự nhiên a và b sao cho :
a) 13< a < b < 16 ;
b) 13 < a < b < 17.
Giải.
a) Vì 13 < 14 < 15 < 16 nên a = 14, b = 15.
b) Ta có các trường hợp sau :
Vì 13 < 14< 15 < 17 nên a = 14, b = 15
Vì 13 < 14 < 16 < 17 nên a = 14, b= 16
Vì 13 < 15 < 16 < 17 nên a = 15 b= 16.
Ví dụ 3. Tính nhanh :
A = 34+ 19 + 21 +46;
B = 103 + 931 +588 + 297+ 12;
C = 25.7.4 + 2.23.50.
Giải.
A = 34 + 19 + 21 + 46
= (34+ 46)+ (19+ 21)
= 80 + 40
= 120.
B = 103 + 931 +588 + 297 + 12
= (103+ 297)+ (588+ 12)+ 931
= 400 + 600 + 931
= 1931.
C = 25 . 7 . 4 + 2 . 23 . 50
= (25 . 4) . 7 + (2 . 50) . 23
= 100 . 7 + 100 . 23
= 100. (7 + 23)
= 3000
Ví dụ 4. So sánh A và B mà không tính cụ thể giá trị của chúng :
a) A = 3214 + 5789 ; B = 5765 + 3238.
b) A = 2011 .2011 ; B = 2010.2012.
Giải.
a) Cách 1: A = 3214 + 5789 = (3214 + 24) + (5789 - 24) = 3238 + 5765 = B.
Vậy A = B.
Cách 2: A = 3214 + 5789 = 3214 + (24 + 5765) = (3214 + 24) + 5765
= 3238 + 5765 = B
b) A = 2011 .2011 = 2011 .(2010+ l) = 2011.2010 + 2011 (1).
B = 2010.2012 = 2010. (2011 + 1) = 2010.2011 +2010 (2).
So sánh (1) và (2) ta thấy A lớn hơn B.
Ví dụ 5. Tính nhanh tổng của 51 số tự nhiên đầu tiên.
Giải. Gọi s là tổng của 51 số tự nhiên đầu tiên. Ta có :
S = 0 + 1 + 2 + 3 + ... + 50.
Gọi S’ là tổng của 50 số tự nhiên từ 1 đến 50.
Ta có: S’ = 1 +2 + 3 + ... + 49 + 50 (1)
S’= 50 + 49 + .... + 2 + 1. (2)
Cộng (1) với (2) và áp dụng tính chất giao hoán và kết hợp của phép cộng ta được :
S’ + S’ = (1 + 50) + (2 + 49) + .... + (49 + 2) + (50 + 1)
= 51 +51 +... + 51 +51.
Do đó 2S‘ = 51 . 50 suy ra S' = 51 . 50 : 2 = 1275.
Vậy S = 0 + S'= 0 + 1275 = 1275.
Ví dụ 6. Tìm số tự nhiên X, biết:
a) (x - 37). 25 = 0 ;
b) (x - 42). (x - 21) = 0.
Giải.
a) Tích (x - 37). 25 bằng 0 mà 25 ≠ 0 nên x - 37 = 0. Suy ra x = 37.
b) Tích (x - 42). (x - 21) bằng 0 nên hoặc x - 42 = 0, hoặc x - 21 =0. Suy ra x = 42 hoặc x = 21.
Ví dụ 7.
a) Cho 8762 + 3974 = A. Không làm phép tính, hãy tìm giá trị của các hiệu
A - 8762 và A - 3974.
b) Cho 7359 - 2897 = B. Không làm phép tính, hãy tìm giá trị của tổng B + 2897 và hiệu 7359 - B.
Giải.
a) 8762 + 3974 = A nên A - 8762 = 3974 và A - 3974 = 8762.
b) 7359 - 2897 = B nên B + 2897 = 7359 và 7359 - B = 2897.
Ví dụ 8. Tìm số tự nhiên x, biết:
a) x : 13 = 21;
b)2125 : x=17;
c) 0 : x = 0 ;
d) x : 5 = x : 6.
Giải.
a) x :13 = 21 b) 2125: x =17
x =13 . 21 x = 2125 : 17
x = 273. x =125.
c) 0 : x = 0
X là số tự nhiên bất kì khác 0.
d) x : 5 = x : 6 (1)
Nhân hai vế của (1) với 30 ta được :
(1) <=> 6x = 5x <=> 6x - 5x = 0 <=> x = 0.
Ví dụ 9. Viết kết quả các phép tính sau dưới dạng một luỹ thừa :
a) 54 . 52;
b) 28.28 ;
c) 365.62;
d) 54 : 52;
e) 28 : 28 ;
g) 365 : 62.
Giải.
a) 54.52 = 54 + 2 = 56
b) 28.28 = 28+8 = 216
c) 365.62 = 365. 36 = 365+1 = 366.
d) 54 : 52 = 54-2 = 52.
e) 28 : 28 = 28-8 = 20.
g) 365 : 62 = 365 : 36 = 365-1 = 364.
Ví dụ 10. Tính giá trị của biểu thức :
A = 120 + 20: 4 - 22. 3;
B = (120 + 20): 4 - 22.3.
C = 120 +(20 : 4 - 22 ). 3;
D = (120 + 20 : 4 - 22). 3.
Giải:
A = 120 + 20 : 4 - 22. 3 = 120 + 5-4.3
= 120 + 5-12
= 125 - 12
= 113.
B = (120 + 20): 4 - 22.3
= 140 : 4 - 4.3
= 35 - 12
= 23.
C = 120 + (20 : 4 -22). 3
= 120+ (5-4). 3
= 120 + 3
= 123.
D = (120 + 20 : 4 - 22). 3
= (120 + 5 - 4) .3
= 121 . 3
= 363
C. BÀI TẬP
1. Điền vào chỗ trông để được ba số tự nhiên liên tiếp tăng dần :
a)....; 27 ;....
b) 15; …. ;....
c) ....; ….. ; 92
d)....; …. ; a + 3 (a ∈ N).
2. Viết tập hợp bốn số tự nhiên liên tiếp lớn hơn 25 nhưng không vượt quá 31.
3. Số 400 là số:
A) Có số chục là 0 ;
(B) Có số đơn vị là 0 ;
(C) Có chữ số hàng chục là 0 ;
(D) Có chữ số hàng chục là 40.
Hãy chọn phương án đúng.
4. Với bài toán : Viết tích 12.5.6 thành tích của ba số tự nhiên khác, một học sinh đã viết các kết quà sau :
(A) 1 . 10.36 ;
(B) 3 . 8 . 15;
(C) 3. 10 . 12 ;
(D) 2 . 10 . 16.
Hãy chỉ ra kết quả sai.
5. Tính nhẩm :
a) 28.25 ;
b) 125.72;
B. MỘT SỐ VÍ DỤ
Ví dụ 1. Tìm số tự nhiên x, biết:
a) x < 3 ;
b) 2 < x ≤ 5;
c) x là số chẵn sao cho 12 < x < 20;
d) x ∉ ℕ*
Giải.
a) x ∈ N và x < 3 nên x ∈ {0; 1 ;2}.
b) x ∈ N và 2 < x ≤ 5 nên x ∈ {3 ; 4 ; 5}.
c) x là số chẵn và 12 ≤ x < 20 nên x ∈ {12 ; 14 ; 16 ; 18}.
d) x ∈ ℕ và x ∉ ℕ* nên x = 0.
Ví dụ 2. Tìm các số tự nhiên a và b sao cho :
a) 13< a < b < 16 ;
b) 13 < a < b < 17.
Giải.
a) Vì 13 < 14 < 15 < 16 nên a = 14, b = 15.
b) Ta có các trường hợp sau :
Vì 13 < 14< 15 < 17 nên a = 14, b = 15
Vì 13 < 14 < 16 < 17 nên a = 14, b= 16
Vì 13 < 15 < 16 < 17 nên a = 15 b= 16.
Ví dụ 3. Tính nhanh :
A = 34+ 19 + 21 +46;
B = 103 + 931 +588 + 297+ 12;
C = 25.7.4 + 2.23.50.
Giải.
A = 34 + 19 + 21 + 46
= (34+ 46)+ (19+ 21)
= 80 + 40
= 120.
B = 103 + 931 +588 + 297 + 12
= (103+ 297)+ (588+ 12)+ 931
= 400 + 600 + 931
= 1931.
C = 25 . 7 . 4 + 2 . 23 . 50
= (25 . 4) . 7 + (2 . 50) . 23
= 100 . 7 + 100 . 23
= 100. (7 + 23)
= 3000
Ví dụ 4. So sánh A và B mà không tính cụ thể giá trị của chúng :
a) A = 3214 + 5789 ; B = 5765 + 3238.
b) A = 2011 .2011 ; B = 2010.2012.
Giải.
a) Cách 1: A = 3214 + 5789 = (3214 + 24) + (5789 - 24) = 3238 + 5765 = B.
Vậy A = B.
Cách 2: A = 3214 + 5789 = 3214 + (24 + 5765) = (3214 + 24) + 5765
= 3238 + 5765 = B
b) A = 2011 .2011 = 2011 .(2010+ l) = 2011.2010 + 2011 (1).
B = 2010.2012 = 2010. (2011 + 1) = 2010.2011 +2010 (2).
So sánh (1) và (2) ta thấy A lớn hơn B.
Ví dụ 5. Tính nhanh tổng của 51 số tự nhiên đầu tiên.
Giải. Gọi s là tổng của 51 số tự nhiên đầu tiên. Ta có :
S = 0 + 1 + 2 + 3 + ... + 50.
Gọi S’ là tổng của 50 số tự nhiên từ 1 đến 50.
Ta có: S’ = 1 +2 + 3 + ... + 49 + 50 (1)
S’= 50 + 49 + .... + 2 + 1. (2)
Cộng (1) với (2) và áp dụng tính chất giao hoán và kết hợp của phép cộng ta được :
S’ + S’ = (1 + 50) + (2 + 49) + .... + (49 + 2) + (50 + 1)
= 51 +51 +... + 51 +51.
Do đó 2S‘ = 51 . 50 suy ra S' = 51 . 50 : 2 = 1275.
Vậy S = 0 + S'= 0 + 1275 = 1275.
Ví dụ 6. Tìm số tự nhiên X, biết:
a) (x - 37). 25 = 0 ;
b) (x - 42). (x - 21) = 0.
Giải.
a) Tích (x - 37). 25 bằng 0 mà 25 ≠ 0 nên x - 37 = 0. Suy ra x = 37.
b) Tích (x - 42). (x - 21) bằng 0 nên hoặc x - 42 = 0, hoặc x - 21 =0. Suy ra x = 42 hoặc x = 21.
Ví dụ 7.
a) Cho 8762 + 3974 = A. Không làm phép tính, hãy tìm giá trị của các hiệu
A - 8762 và A - 3974.
b) Cho 7359 - 2897 = B. Không làm phép tính, hãy tìm giá trị của tổng B + 2897 và hiệu 7359 - B.
Giải.
a) 8762 + 3974 = A nên A - 8762 = 3974 và A - 3974 = 8762.
b) 7359 - 2897 = B nên B + 2897 = 7359 và 7359 - B = 2897.
Ví dụ 8. Tìm số tự nhiên x, biết:
a) x : 13 = 21;
b)2125 : x=17;
c) 0 : x = 0 ;
d) x : 5 = x : 6.
Giải.
a) x :13 = 21 b) 2125: x =17
x =13 . 21 x = 2125 : 17
x = 273. x =125.
c) 0 : x = 0
X là số tự nhiên bất kì khác 0.
d) x : 5 = x : 6 (1)
Nhân hai vế của (1) với 30 ta được :
(1) <=> 6x = 5x <=> 6x - 5x = 0 <=> x = 0.
Ví dụ 9. Viết kết quả các phép tính sau dưới dạng một luỹ thừa :
a) 54 . 52;
b) 28.28 ;
c) 365.62;
d) 54 : 52;
e) 28 : 28 ;
g) 365 : 62.
Giải.
a) 54.52 = 54 + 2 = 56
b) 28.28 = 28+8 = 216
c) 365.62 = 365. 36 = 365+1 = 366.
d) 54 : 52 = 54-2 = 52.
e) 28 : 28 = 28-8 = 20.
g) 365 : 62 = 365 : 36 = 365-1 = 364.
Ví dụ 10. Tính giá trị của biểu thức :
A = 120 + 20: 4 - 22. 3;
B = (120 + 20): 4 - 22.3.
C = 120 +(20 : 4 - 22 ). 3;
D = (120 + 20 : 4 - 22). 3.
Giải:
A = 120 + 20 : 4 - 22. 3 = 120 + 5-4.3
= 120 + 5-12
= 125 - 12
= 113.
B = (120 + 20): 4 - 22.3
= 140 : 4 - 4.3
= 35 - 12
= 23.
C = 120 + (20 : 4 -22). 3
= 120+ (5-4). 3
= 120 + 3
= 123.
D = (120 + 20 : 4 - 22). 3
= (120 + 5 - 4) .3
= 121 . 3
= 363
C. BÀI TẬP
1. Điền vào chỗ trông để được ba số tự nhiên liên tiếp tăng dần :
a)....; 27 ;....
b) 15; …. ;....
c) ....; ….. ; 92
d)....; …. ; a + 3 (a ∈ N).
2. Viết tập hợp bốn số tự nhiên liên tiếp lớn hơn 25 nhưng không vượt quá 31.
3. Số 400 là số:
A) Có số chục là 0 ;
(B) Có số đơn vị là 0 ;
(C) Có chữ số hàng chục là 0 ;
(D) Có chữ số hàng chục là 40.
Hãy chọn phương án đúng.
4. Với bài toán : Viết tích 12.5.6 thành tích của ba số tự nhiên khác, một học sinh đã viết các kết quà sau :
(A) 1 . 10.36 ;
(B) 3 . 8 . 15;
(C) 3. 10 . 12 ;
(D) 2 . 10 . 16.
Hãy chỉ ra kết quả sai.
5. Tính nhẩm :
a) 28.25 ;
b) 125.72;
c) 99 + 59 ;
d) 457 - 98.
6. Nêu ba cách tính nhẩm 600 : 12.
7. Đố vui: Bé Nam rất không thích tính nhẩm. Khi giải bài toán chia đều 40 cái kẹo cho 8 bạn, bé đã viết tính chia như sau :
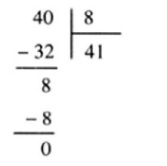 Kết quả tìm được đã làm bé Nam bối rối. Bé hiểu rõ là mỗi bạn khống thể nhận được số kẹo nhiều hơn số kẹo của cả 8 bạn nhưng bé không hiểu sai lầm trong phép chia là ở đâu. Đố em phát hiện ra chỗ sai ?
8. "Hai lần hai là năm".
Ta có đằng thức hiển nhiên : 4 : 4 = 5 : 5. (1)
Đưa ra ngoài dấu ngoặc thừa số chung của mỗi vế ở đẳng thức (1) ta sẽ có :
4. (1 : 1) = 5.(1 : 1)
hay (2.2).(1 : 1) = 5.(1 : 1). (2)
Vì 1 : 1 = 1 nên đẳng thức (2) trở thành :
2 . 2 = 5 (!).
Em có biết sai ở đâu không ?
9. Dùng năm chữ số giống nhau, dấu các phép tính, dấu ngoặc để viết biểu thức có giá trị bằng 100.
10. Trong các nhà máy luyện kim hay nhà máy gỗ, những ống thép hay cây gỗ tròn thường được xếp rất đều đặn như hình 1
Kết quả tìm được đã làm bé Nam bối rối. Bé hiểu rõ là mỗi bạn khống thể nhận được số kẹo nhiều hơn số kẹo của cả 8 bạn nhưng bé không hiểu sai lầm trong phép chia là ở đâu. Đố em phát hiện ra chỗ sai ?
8. "Hai lần hai là năm".
Ta có đằng thức hiển nhiên : 4 : 4 = 5 : 5. (1)
Đưa ra ngoài dấu ngoặc thừa số chung của mỗi vế ở đẳng thức (1) ta sẽ có :
4. (1 : 1) = 5.(1 : 1)
hay (2.2).(1 : 1) = 5.(1 : 1). (2)
Vì 1 : 1 = 1 nên đẳng thức (2) trở thành :
2 . 2 = 5 (!).
Em có biết sai ở đâu không ?
9. Dùng năm chữ số giống nhau, dấu các phép tính, dấu ngoặc để viết biểu thức có giá trị bằng 100.
10. Trong các nhà máy luyện kim hay nhà máy gỗ, những ống thép hay cây gỗ tròn thường được xếp rất đều đặn như hình 1
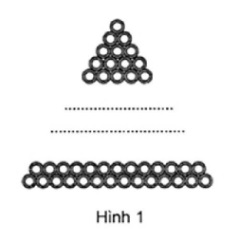 Xếp như vậy không những dẹp mắt mà lại còn đếm rất tiện.
Ví dụ : Có một đống ống thép có kích thước như nhau, anh công nhân chỉ cần đếm xem ở đáy có bao nhiêu ống là lập tức có thế biết đống thép ấy có bao nhiêu ống.
a) Nếu hàng dưới cùng có 30 ống thép, hàng ngay trên nó có 29 ống, hàng trên tiếp theo có 28 ống .... hàng trên cùng chỉ có 1 ống thì tất cả có bao nhiêu ống thép ?
b) Nếu hàng dưới cùng có 30 ống thép và cũng xếp như ở câu a) nhưng hàng trên cùng có 17 ống thì tất cả có bao nhiêu ống thép ?
Xếp như vậy không những dẹp mắt mà lại còn đếm rất tiện.
Ví dụ : Có một đống ống thép có kích thước như nhau, anh công nhân chỉ cần đếm xem ở đáy có bao nhiêu ống là lập tức có thế biết đống thép ấy có bao nhiêu ống.
a) Nếu hàng dưới cùng có 30 ống thép, hàng ngay trên nó có 29 ống, hàng trên tiếp theo có 28 ống .... hàng trên cùng chỉ có 1 ống thì tất cả có bao nhiêu ống thép ?
b) Nếu hàng dưới cùng có 30 ống thép và cũng xếp như ở câu a) nhưng hàng trên cùng có 17 ống thì tất cả có bao nhiêu ống thép ?
HƯỚNG DẪN GIẢI
1. a) 26; 27; 28.
b) 15; 16; 17.
c) 90; 91; 92.
d) a + 1 ; a + 2 ; a + 3.
2. Các tập hợp phải tìm là :
A = {26; 27; 28; 29} ;
B = |27;28; 29; 30} ;
C = {28 ; 29 ; 30 ; 31}.
3. Chọn (C).
4. Kết quả sai là (D).
5. a) 28.25 = (7 . 4) . 25 = 7 . (4 . 25) = 7 . 100 = 700.
b) 125 . 72= 125 . (8 . 9) = (125 . 8) . 9= 1000 . 9 = 9000.
c) 99 + 59 = (99 + l) + (59 - 1)= 100 + 58= 158.
d) 457 - 98 = (457 + 2) - (98 + 2) = 459 - 100 = 359.
Lưu ý. Khi thực hiện tính nhẩm như trên, ta đã áp dụng các tính chất sau :
- Tính chất kết hợp của phép nhân (câu a) và câu b).
- Tổng của hai số khỏng đổi nếu ta thêm vào ở số hạng này và bớt đi ở số hạng kia cùng một số đơn vị.
- Hiệu của hai số không đổi nếu ta thêm vào số bị trừ và số trừ cùng một số đơn vị.
6.
Cách 1: 600 : 12 = (60 . 10) : 12 = (60 : 12). 10 = 5 . 10 = 50.
Cách 2: 600 : 12 = 600 : (3 . 4) = (600 : 3) : 4 = 200 : 4 = 50.
Cách 3: 600: 12 = (480 + 120) : 12 = 480 : 12+ 120 : 12 = 40+ 10 = 50.
Lưu ý: Trong các cách nhẩm trên, ta đã áp dụng các tính chất của phép chia.
Cách 1 : Tính chất một tích chia cho một số:
(a . b): c = (a : c). b = a . (b : c)
Cách 2 : Tính chất một số chia cho tích :
a : (b . c) = (a : b): c = (a : c): b.
Cách 3 : Tính chất một tổng chia cho một số:
(a + b) : c = a : c + b : c
7.
Bé Nam đã làm phép chia như sau :
40: 8 = (32 + 8) : 8 = 32 : 8 + 8 : 8 = 4 + 1.
Nhưng vì bé đã viết không đúng khi tính đơn vị của số hạng thứ nhất, bé đã đưa sang hàng chục nên 4 + 1 đã thành 4 . 10 + 1 = 41. Sai lầm là ở chỗ đó.
8.
Sai lầm từ chỗ đưa thừa số chung ra ngoài dấu ngoặc :
4 : 4 không phải là 4 . (1 : 1) mà là 4 . (1 : 4).
Thật vậy 4 : 4 = 44 = 4 . 14
= 4 . 14 = 4.(1 : 4).
9.
Cách 1 : 33.3 + 3 : 3 = 99 + 1 = 100.
Cách 2: 111 - 11 = 100.
Cách 3: 5. (5 + 5 + 5 + 5) = 5 . 20= 100.
Cách 4 : 5 . 5 . 5 – 5 . 5 = 125 - 25 =100.
Cách 5 : 99 + 99 - 9 = 99 + 90= 99 + 1 = 100.
10.
a) Tổng số ống thép là
= 4.(1 : 4).
9.
Cách 1 : 33.3 + 3 : 3 = 99 + 1 = 100.
Cách 2: 111 - 11 = 100.
Cách 3: 5. (5 + 5 + 5 + 5) = 5 . 20= 100.
Cách 4 : 5 . 5 . 5 – 5 . 5 = 125 - 25 =100.
Cách 5 : 99 + 99 - 9 = 99 + 90= 99 + 1 = 100.
10.
a) Tổng số ống thép là 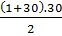 = 465
b) Tổng số ống thép là
= 465
b) Tổng số ống thép là 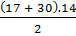 = 329.
= 329.
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.