Ôn tập hè Toán 6 bài 2: Tính chất chia hết. Ước và bội. Số nguyên tố. Hợp số. Ước chưng, bội chung

A. KIẾN THỨC CƠ BẢN
1. Định nghĩa
• a ⋮ b ⇔ a = b. k ⇔ a ∈ Ư(a) (a, b, k ∈ (a) (a, b, k ∈ ℕ, b ≠ 0).
• Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
• Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
• Ước chung của hai hay nhiều số là ước của tất cả các số đó :
x ∈ ƯC(a, b) nếu a ⋮ x, b ⋮ x.
• Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong các ước chung của các số đó :
ƯCLN (a, b) = d nếu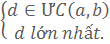
• Bội chung của hai hay nhiều số là bội của tất cả các số đó :
x ∈ BC (a, b) nếu x ⋮ a, x ⋮ b.
Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó :
BCNN(a, b) = m nếu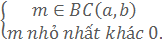
2. Tính chất chia hết
• Tính chất 1:      a ⋮ m, b ⋮ m => (a + b) ⋮ ni và (a - b) ⋮ m
                            a ⋮ m, b ⋮ m, c ⋮ m => (a + b + c) ⋮ m
• Tính chất 2 :     a ⋮̸ m, b ⋮ m => (a + b) ⋮̸ m và (a - b) ⋮̸ m
                            a ⋮̸ m, b ⋮ m, c ⋮ m => (a + b + c) ⋮̸ m
3. Các dấu hiệu chia hết
a ⋮ 2 ⇔ a có chữ số tân cùng bàng một trong các chữ số : 0, 2, 4, 6, 8.
a ⋮ 5 ⇔ a có chữ số tân cùng bàng 0 hoặc bằng 5.
a ⋮ 9 ⇔ a có tổng các chữ số chia hết cho 9.
a ⋮ 3 ⇔ a có tổng các chữ số chia hết cho 3.
4. Cách tìm ƯCLN và BCNN

B. MỘT SỐ VÍ DỤ
Ví dụ 1. Không tính giá trị của biểu thức, hãy xét xem các tổng sau có chia hết cho 3 không ?
A= 18 + 27+123
B= 15 + 32 + 78
C = 44 + 40 + 300.
Giải. Tổng A có 18 ⋮ 3, 27 ⋮ 3, 123 ⋮ 3 nên A ⋮ 3 (Tính chất 1).
Tổng B có 15 ⋮ 3. 32 ⋮̸ 3, 78 ⋮ 3 nên B ⋮̸ 3 (Tính chất 2).
C = 44+ 40+ 300 = (44+ 1) + (40 - l) + 300
   = 45 + 39 + 300.
Do đó C có 45 ⋮ 3, 39 ⋮ 3, 300 ⋮ 3 nên C ⋮ 3 (Tính chất 1).
Ví dụ 2. Khi chia số a cho 24 ta được số dư là 16. Hỏi:
a) Số a có chia hết cho 8 không ?
b) Số a có chia hết cho 6 không ?
Giải. Số a chia cho 24 dư 16 nên ta có :
a = 24k + 16 (k ∈ N ).
a) Vì 24k ⋮ 8 và 16 ⋮ 8 nên (24k + 16) ⋮ 8. Vậy số a chia hết cho 8.
b) 24k ⋮ 6 nhưng 16 ⋮̸ 6 nên (24k + 16) ⋮̸  6. Vậy số a không chia hết cho 6.
Ví dụ 3. Chứng tỏ rằng số có dạng 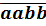 bao giờ cũng chia hết cho 11.
Giải. Cách 1: 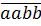 = l000a + 100a + 10b + b = 1100a + 1 lb
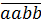Ta có 1100a ⋮ 11,11b ⋮ 11 nên (1100a + 11b) ⋮ 11 hay số có dạng  bao giờ cũng chia hết cho 11.
Cách 2. 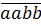 =  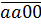+  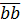= (a.1100 + b.11) ⋮ 11.
Cách 3. 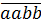 =  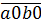+  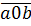= 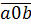. 10 +  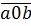= 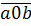. 11⋮ 11.
Ví dụ 4. Thay dấu * bởi chữ số thích hợp để số 59* :
a) Chia hết cho 2 ;
b) Chia hết cho 5 ;
c) Chia hết cho cả 2 và 5 ;
d) Không chia hết cho cả 2 và 5 ;
c) Chia hết cho 3 mà không chia hết cho 9;
g) Chia hết cho 9.
Giải.
a) Thay dấu * bởi các chữ số 0, 2, 4, 6, 8 ta dược các số chia hết cho 2 là : 590; 592; 594 ; 596 ; 598.
b) Thay dấu * bởi các chữ số 0, 5 ta dược các số chia hết cho 5 là : 590; 595.
c) Thay dấu * bởi chữ số 0 ta được số 590 chia hết cho cả 2 và 5.
d) Thay dấu * bởi các chữ số 1, 3, 7, 9 ta được các số không chia hết cho cả 2 và 5 là : 591 ; 593 : 597 ; 599
c) Thay dấu * bởi các chữ số 1,7 ta được các số chia hết cho 3 mà không chia hết cho 9 là: 591 ; 597.
g) Thay dấu * bởi chữ số 4 ta được số 594 chia hết cho 9.
Ví dụ 5. Dùng ba trong bốn chữ số 1, 2, 6, 7 để viết tất cả các số tự nhiên co ba chữ số chia hết cho cả ba số 2 ; 3 ; 9.
Giải. Ta chọn ba chữ số có tổng chia hết cho 9, đó là 1, 2, 6. Các số dược viết bằng ba chữ số này vừa chia hết cho 3, vừa chia hết cho 9.
Để viết số chia hết cho 2, ta đặt chữ số 2 hoặc 6 ở vị trí tận cùng.
Nếu chữ số tận cùng là 2, ta có hai số: 612, 162.
Nếu chữ số tận cùng là 6, ta có hai số: 216, 126.
Vậy ta viết dược tất cả bốn số: 612, 162, 216, 126.
Ví dụ 6. Tìm các số tự nhiên x sao cho :
a) x ∈ B (11) và 30 < x < 70 ;
b) x ∈ Ư (20) và x > 4.
Giải.
a) Do x ∈ B (11) nên x = 11 k (k ∈ N). Vì 30 < x < 70 nên k ∈ {3 ; 4; 5 ; 6 }.
Do dó x ∈ {11 .3 ; 11 . 4 ; 11 . 5 ; 11, 6} tức là x ∈ {33 ; 44 ; 55 ; 66}.
b) Do x ∈ Ư(20) nên x ∈ {l;2;4;5;10; 20).
Vì x lớn hơn 4, vậy x ∈ {5 ; 10 ; 20}.
Ví dụ 7. Trong các số sau, số nào là số nguyên tố, số nào là hợp số: 0 ; 1 ; 91 ; 97; 561; 1287?
Giải. Số 0 và số 1 không là số nguyên tố và cũng không là hợp số.
Số 97 là số nguyên tố vì 97 lớn hơn 1 và chỉ có hai ước là 1 và chính nó.
Số 91 là hợp số vì 91 lớn hơn 7 và chia hết cho 7.
Số 561 là hợp số vì 561 lớn hơn 3 và chia hết cho 3.
Số 1287 là hợp số vì 1287 lớn hơn 3 và chia hết cho 3.
Ví dụ 8. Thay dấu * bằng chữ số thích hợp để được hợp số:
a)  ;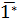
b)  .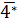
Giải.
a) Trong các số có dạng 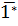  có 11, 13, 17, 19 là số nguyên tố, các số còn lại đều là hợp số. Do đó 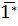∈ {10; 12; 14 ; 15 ; 16; 18).
b) Trong các số có dạng 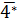 có 41,43, 47 là số nguyên tố, các số còn lại đều là hợp số. Do đó 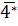∈ {40 ; 42 ; 44 ; 45 ; 46 ; 48 ; 49|.
Ví dụ 9. Tìm ước chung lớn nhất của 648 và 540 rồi tìm tất cả các ước chung của 648 và 540.
Giải. Phân tích ra thừa số nguyên tố :
648 = 2³. 3⁴
540 = 2². 3³.5
ƯCLN (648 ; 540) = 2². 3³ = 108.
Vì ước chung của 648 và 540 chính là ước của ƯCLN(648 ; 540) nên ta có : ƯC(648 ; 540) = Ư(108) = {1 ; 2 ; 3 ; 4 ; 6; 9; 12; 18 ; 27 ; 36; 54 ; 108}.
Ví dụ 10. Tìm các bội chung nhỏ hơn 2000 của ba số 68, 85 và 170.
Giải. Ta có nhận xét 170.2 = 340 ; 340 : 68 và 340 : 85 nên
BCNN(68 ; 85 ; 170) = 340.
Để tìm bội chung của ba số 68 ; 85 và 170 ta chỉ việc nhân
BCNN(68 ; 85 ; 170) lần lượt với 0 ; 1 ; 2 ; 3 ;
Ta có BC(68 ; 85 ; 170) = {0 ; 340 ; 680 ; 1020 ; 1360 ; 1700 ; 2040 ;...)
Các bội chung nhỏ hơn 2000 của 68 ; 85 và 170 là 0 ; 340 ; 680 ; 1020 ; 1360 và 1700.

C. BÀI TẬP
1. Không tính giá trị của biểu thức, hãy xét xem các tổng sau có chia hết cho 7 không ?
A =14+ 35+ 63 ;
B = 21 +42+ 50;
C = 17 + 31+57.
2. Khi chia số a cho 18 ta được số dư là 6. Hỏi:
a) Số a có chia hết cho 6 không ?
b) Số a có chia hết cho 9 không ?
3. Không tính giá trị của biểu thức, hãy xét xem các hiệu sau có chia hết cho 9 không ?
A = 423 -198;
B = 620 - 594;
C = 134 - 98.
4. Dùng cả ba chữ số 8, 0, 5 để ghép thành các số tự nhiên có ba chữ số chia hết cho 5. Số các số như trên có thể lập được là :
(A) l;
(B) 2;
(C) 3;
(D) 4.
Hãy chọn phương án đúng.
5. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
(A) Số chia hết cho 3 thì chia hết cho 9 ;
(B) Số chia hết cho 9 thì chia hết cho 3 ;
(C) Số chia hết cho 5 thì tận cùng bằng 5 ;
(D) Số tận cùng bằng 0 thì chia hết cho 2.
6. Số 13 là số nguyên tố có tính chất: nếu đổi chỗ hai chữ số của nó thì ta lại được một số nguyên tố, đó là số 31. Trong các số nguyên tố nhỏ hơn 100, những số nào cũng có tính chất như số 13?
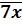7. Để  là hợp số, chữ số x là :
(A) 1 ;
(B) 3;
(C) 7;
(D) 9
Hãy chọn phương án đúng.
8. Tổng của hai số nguyên tố có thể bằng 4025 được không ?
9. Tìm số tự nhiên x, biết rằng 403 chia cho x thì dư 12, còn 217 chia cho x thì dư 13.
10. Người ta đem trứng trong một rổ. Nếu đem theo từng chục cũng như đem theo tá (12 quả) hoặc đem từng 15 quả một thì lần nào cũng còn lại 1 quả. Tính số trứng trong rổ, biết ràng số trứng chưa đến 100.

HƯỚNG DẪN GIẢI

1. Vì 14 ⋮ 7, 35 ⋮ 7, 63 ⋮ 7 nên A ⋮ 7.
Vì 21 ⋮ 7, 42 ⋮ 7, 50 ⋮̸ 7 nên B ⋮̸ 7.
Ta viết C = 17 + 31 +57 = (17 + 4)+ (31 - 3)+ (57- 1)
                = 21 +28 + 56.
Vì 21 ⋮ 7, 28 ⋮ 7, 56 ⋮ 7 nên C ⋮ 7.
2. a) a chia hết cho 6.
b) a không chia hết cho 9.
3. A ⋮ 9, B ⋮̸  9, C = 134 - 98 = (134+ 1) - (98 + 1)
                            = (135 -99) ⋮ 9.
4. Chọn (C).
5. (A) sai; (B) đúng ; (C) sai; (D) đúng.
6. Đó là các số 11 ; 17 và 71 ; 37 và 73 ; 79 và 97.
7. Chọn (C).
8. Số 4025 là một số lẽ. Nếu tổng của hai số nguyên tố bằng 4025 thì một trong hai số nguyên tố phải là 2. Khi đó số kia là 4025 - 2 = 4023 mà 4023 là hợp số (vì lớn hơn 3 và chia hết cho 3). Vậy tổng của hai số nguyên tố không thể là 4025.
9. 403 chia cho x dư 12 nên (403 - 12) ⋮ x hay 391 ⋮ x và x > 12 (1).
    217 chia cho x dư 13 nên (217 - 13) ⋮ x hay 204 ⋮ x và x > 13 (2).
Từ (1), (2) suy ra x ∈ ƯC (391 ; 204) và x > 13.
ƯCLN (391, 204) = 17.
x ∈ Ư ( 17) và x > 13. Vậy x = 17.
10. Số trứng trong rổ bớt đi 1 quả là bội chung của 10, 12 và 15.
BCNN (10 ; 12 ; 15) = 60. Vì số trứng chưa đến 100 nên số trứng trong rổ là 60 + 1 = 61 (quả).