A. KIẾN THỨC CỞ BẢN
1. Tập hợp gồm các số nguyên âm, số 0 và các số nguyên dương gọi là tập hợp các số nguyên, kí hiệu là Z.
Z = {...;-3; -2; -l; 0; 1; 2; 3;... }.
2. Khoảng cách từ điểm a đến điểm 0 trên trục số là giá trị tuyệt đối của số nguyên a, kí hiệu là |a| .
Nếu a = 0 thì |a| = 0. Nếu a > 0 thì |a| = a. Nếu a < 0 thì |a| = -a.
3. Trong hai số nguyên âm, số nào có giá trị tuyệt đối (GTTĐ) nhỏ hơn thì số đó lớn hơn.
4. Cộng hai số nguyên.
a) Nếu một trong hai số bằng 0 thì tổng bằng số còn lại.
b) Muốn cộng hai số nguyên cùng dấu, ta cộng hai GTTĐ với nhau, còn dấu là dấu chung.
c) Hai số nguyên đối nhau có tổng bằng 0.
d) Muốn cộng hai số nguyên khác dấu không đối nhau, ta lấy GTTĐ lớn trừ GTTĐ nhỏ, rồi đặt trước kết quả tìm được dấu của số có GTTĐ lớn.
Tính chất của phép cộng các số nguyên :
Giao hoán : a + b = b + a ;
Kết hợp : (a + b) + c = a + (b + c);
Cộng với số 0 : a + 0 = 0 + a = a ;
Cộng với số đối : a + (-a) = 0.
5. Trừ hai số nguyên
Muốn trừ số nguyên a cho số nguyên b ta cộng a với số đối của b.
a - b = a + (- b)
6. Quy tắc dấu ngoặc
Khi bỏ dấu ngoặc có dấu đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc.
Trong một tổng đại số, ta có thể:
- Thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.
- Đặt dấu ngoặc để nhóm các số hạng một cách tùy ý theo quy tắc dấu ngoặc nêu ở trên.
7. Quy tắc chuyển vế
Khi chuyển một số hạng từ về này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.
8. Nhân hai số nguyên
a) Nếu một trong hai thừa số bằng 0 thì tích bằng 0.
b) Muốn nhân hai số nguyên cùng dấu, ta nhân hai GTTĐ của chúng.
c) Muốn nhân hai số nguyên khác dấu, ta nhân hai GTTĐ của chúng, rồi đặt dấu trước kết quả.
Tính chất của phép nhân các số nguyên :
Giao hoán : a . b = b . a.
Kết hợp : (a . b). c = a . (b . c).
Nhân với số 1 : a . 1 = 1 . a = a.
Phân phối của phép nhân đối với phép cộng : a . (b + c) = ab + ac.
• Khi nhân nhiều thừa số khác 0, cần nhớ quy tắc về dấu
- Nếu số thừa số âm chẵn thì tích là số dương.
- Nếu số thừa số âm lẻ thì tích là số âm.
9. Bội và ước của một số nguyên.
a ⋮ b ⇔ a = b . k ⇔ a là bội của b ⇔ b là ước của a
(a, b, k ∈ Z, b ≠ 0).
Các tính chất chia hết cần nhớ :
a ⋮ b và b ⋮ c => a ⋮ c
a ⋮ b => a . m ⋮ b (m ∈ Z)
a ⋮ c và b ⋮ c => (a + b) ⋮ c
a ⋮ c và b ⋮̸ c => (a + b) ⋮̸ c.
B. MỘT SỐ VÍ DỤ
Ví dụ 1. Điền dấu "+" hoặc dấu “-” vào chỗ trống (...) để được kết quả đúng :
a) 0 >.... 3;
b) 0 <.... 7;
c) .... 6 > .... 7 ;
d).... 12 < .... 5.
Giải.
a) 0 > -3 ;
b) 0 < +7 ;
c) + 6 > -7 ; hoặc - 6 > -7 ;
d) -12 < + 5 hoặc - 12 < -5.
Ví dụ 2. Điền dấu "+" hoặc dấu “-” vào chỗ trống (...) để được kết quả đúng :
a) (....20) + (...3) = (....23);
b) (.... 20) + (....3) = (....17).
Giải.
a) Cách 1 : (+20) + (+ 3) = (+23); Cách 2: (-20) + (-3) = (-23).
b) Cách 1 : (+ 20) + (-3) = (+17); Cách 2 : (-20) + (+3) = (-17).
Ví dụ 3. Vận dụng tính chất giao hoán và kết hợp để tính các tổng sau :
A = 89 + (-36) + (-8) + 29 + 15 + (-34)
B = 407 + (-689) + (-207) + 489.
Giải.
A = 89 + (-36) + (-8) + 29 + 15 + (-34)
= (89 + 29 + 15) + ((-36) + (- 34) + (-8)]
= 133+ (-78)
= 55.
B = 407 + (-689) + (-207) + 489.
= [407 + (-207) ] + [(-689) + 489]
= 200 +(-200)
= 0.
Ví dụ 4. Một thủ quỹ ghi số tiền thu chi trong ngày (đơn vị nghìn đồng), thu ứng với dấu "+", chi ứng với dấu “-” như sau : + 215 ; - 530; + 650; - 100; - 85 ; + 400. Đầu ngày trong két có 750 nghìn đồng. Hỏi cuối ngày trong két có bao nhiêu ?
Giải.
Tổng số tiền thu, chi trong ngày là :
(+ 215) + (- 530) + (+ 650) + (- 100) + (- 85) + (+ 400)
= (215 + 650 + 400) + [(- 530 + (- 100) + (- 85)]
= 1265 +(-715)
= 550.
Cuối ngày số tiền có trong két là : 750 + 550 = 1300 (nghìn đổng).
Ví dụ 5. Tìm x, biết:
a) 17-(2 + x) = 3;
b) (6 + x) - (17 - 23) = - 11.
Giải:
a) 17-( 2 + x) = 3
17 – 2 - x = 3
15 - x = 3
15 - 3 = x
x = 12.
b) (6 + x) - (17 - 23) = - 11
6 + x - 17 + 23 = -11
x + 12 = - 11
x = - 11 - 12
x = - 23.
Ví dụ 6. Không thực hiên phép tính, hãy tìm các cặp biểu thức có giá trị bằng nhau:
A = 93 - (278 - 369);
B = 93 - 278 - 369 ;
C = 93 - 369 + 278 ;
D = 93 - (278 + 369);
E = 93 + 369 - 278.
Giải.
A = 93 - (278 - 369) = 93 - 278 + 369 = 93 + 369 - 278 = E.
B = 93 – 278 - 369 = 93 - (278 + 369) = D.
Ví dụ 7. Tìm số nguyên x, biết rằng :
a) |x - 2| = 4 ;
b) |x - 2| < 3.
Giải.
a) |x – 2| = 4 suy ra x - 2 = 4 hoặc x - 2 = - 4
Nếu x - 2 = 4 thì x = 4 + 2 = 6.
Nếu x - 2 = - 4 thì x = -4 + 2 = -2.
Vậy x = 6 hoặc x = - 2.
b) |x – 2| < 3 mà với ∈ Z thì |x - 2| ∈ N, suy ra |x – 2| ∈{0; 1 ; 2).
Nếu |x – 2| =0 thì x - 2 = 0 suy ra x = 2.
Nếu |x – 2| = 1 thì x - 2 = 1 hoặc x - 2 = - 1 suy ra x = 3 hoặc x = 1.
Nếu |x – 2| =2 thì x - 2 = 2 hoặc x - 2 = - 2 suy ra x = 4 hoặc x = 0.
Vậy x ∈ {0; 1 ; 2; 3 ; 4}.
Ví dụ 8. So sánh A và B, biết rằng :
A = (-120). 7. 13 .(-15). (-21). 630;
B = 519 . (-14). 6 . (-12).
Giải.
Trong tích A có 3 thừa số âm nên A < 0 (1).
Trong tích B có 2 thừa số âm nên B > 0 (2).
Từ (1) và (2) suy ra A < B.
Ví dụ 9. Tìm số nguyên x, biết rằng x - 1 là ước của 6.
Giải.
Ta có Ư(6) = {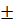 1 ;
1 ; 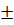 2 ;
2 ; 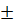 3 ;
3 ; 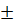 6}.
Do đó x - 1 ∈ {- 6 ; - 3 ; - 2 ; - 1 ; 1 ; 2; 3 ; 6}.
Suy ra x ∈ {- 5 ; - 2 ; - 1 ; 0; 2; 3 ; 4 ; 7}.
Ví dụ 10. Tìm các số nguyên x và y sao cho (x - l)(y + 2) = 5.
Giải.
Ta có x - 1 và y + 2 là các số nguyên và là ước của 5.
Ư(5) = {∈1 ; ∈ 5}. Ta có bảng sau :
6}.
Do đó x - 1 ∈ {- 6 ; - 3 ; - 2 ; - 1 ; 1 ; 2; 3 ; 6}.
Suy ra x ∈ {- 5 ; - 2 ; - 1 ; 0; 2; 3 ; 4 ; 7}.
Ví dụ 10. Tìm các số nguyên x và y sao cho (x - l)(y + 2) = 5.
Giải.
Ta có x - 1 và y + 2 là các số nguyên và là ước của 5.
Ư(5) = {∈1 ; ∈ 5}. Ta có bảng sau :
| x - 1 |
1 |
-1 |
5 |
-5 |
| y + 2 |
5 |
-5 |
1 |
-1 |
Suy ra
C. BÀI TẬP
1. Điền Đ (đúng) hoặc S (sai) vào ô vuông trong mỗi câu sau đây :
a) Nếu a ∈ N thì a ∈ Z □
b) Nếu a ∈ N thì a ∈ N* □;
c) Nếu a ∈ Z thì a ∈ N □;
d) Nếu a ∉ Z thì a ∉ N □
2. Điền số thích hợp vào chỗ trống (...) trong mỗi câu sau đây :
a) Số liền sau của số -5 là ...;
b) Số liền trước của số -2 là ...;
c) Giá trị tuyệt đối của số - 7 là ...;
d) Số đối của 0 là ...
3. Tính giá trị của các biếu thức :
a) |-6| + |+6|;
b) |-5| - |-2|;
c) |-7| . |-4| ;
d) |-5| :| +3|.
4. Tìm số nguyên a biết a + |a| = 4.
5. Tìm tổng các số nguyên x thoả mãn -10 < x < 12.
6. Đặt dấu ngoặc một cách thích hợp để tính nhanh các tổng đại số sau :
A = 879 - 1876+ 1865 - 2879;
B = 6 – 7 – 8 + 9 - 10 + 11 + 12 - 13+ 14- 15- 16 + 17 - 18.
7. Tìm số nguyên x sao cho x . (x + 3) < 0.
8. Trên mặt đồng hồ có 12 số từ 1 đến 12. Em hãy dặt dấu "+", dấu “-” trước các số để tổng đại số của các số ấy bằng 0.
9. Đố vui: Chứng minh 5 = 7 !
Lấy hai số dương tuỳ ý a, b sao cho 2a = 3b. (1)
Từ (1) suy ra 10a = 15b và 14a = 21 b.
Trừ hai đẳng thức này theo từng vế tương ứng ta được :
14a - 10a = 21b - 15b. (2)
Chuyển vế từ (2) ta được :
15b - 10a = 21b - 14a. (3)
Đặt thừa số chung ở mỗi vế của (3):
5(3b - 2a) = 7(3b - 2a). (4)
Chia hai vế của (4) cho (3b - 2a) ta được 5 = 7 (!).
Em hãy giải thích tại sao lại có kết quả vô lí này !
10. Đố vui: Chứng minh : Mọi số đều bằng nhau.
Giả sử a > b thế thì a - b = c (c > 0) hay a = b + c (1).
Nhân hai vế của (1) với (a - b) ta được :
a(a - b) = (a - b)(b + c)
a2 - ab = ab + ac - b2 - bc
a2 - ab - ac = ab - b2 - bc
a(a - b - c) = b(a - b - c). (2)
Chia hai vế của đẳng thức (2) cho (a - b - c) ta được a = b (!).
Đố em tìm được chỗ sai trong chứng minh trên.
ĐÁP ÁN
1. a) Đ;
b) S;
c) S;
d) Đ.
2. a) -4;
b) -3;
c) 7;
d) 0.
3. a) 12;
b) 3;
c) 28 ;
d) 5.
4. Nếu a > 0 thì từ a + |a| = 4 ta có a + a = 4 => 2a = 4 => a = 2.
Nếu a < 0 thì từ a + |a| = 4 ta có a - a = 4 => 0 = 4 (vô lí).
Nếu a = 0 thì từ a + |a| = 4 ta có 0 + 0 = 4 => 0 = 4 (vô lí).
Vậy a = 2.
5. Vì x ∈ Z và -10 < x < 12 nên
x ∈ {-9; -8; -7; -6; -5; - 4; -3;-2;-1; 0; 1; 2; 3;4; 5; 6;7; 8; 9; 10; 11}
Tổng của chúng là :
[(-9) + 9] + [(-8) + 8) + [(-7) + 7] +[(-6) + 6] +[(-5) + 5] +[(-4) + 4] +[(-3) + 3] + [(-2) + 2] + [(-l) + 1] + 0 + (10 + 11) = 0 + 21 =21
6. A = (879 - 2879) - (1876 - 1865) = -2000 - 11 = -2011.
B = (6 - 7 - 8 + 9) - (10 - 11 - 12 + 13) + (14 - 15 - 16 + 17) - 18
= 0 - 0 + 0 - 18 = - 18.
7. Tích x . (x + 3) < 0 nên x và x + 3 trái dấu nhau mà x < x + 3 nên x < 0 và x + 3 > 0 tức là -3 < x < 0, x ∈ Z. Vậy x ∈ {-2 ; -1}.
8. Ta biết rằng hai số đối nhau có tổng bằng 0.
Ta lại có 1 + 2 + 3 + ... + 12 = 78. Do dó, chỉ cần chia 12 số thành hai nhóm, mỗi nhóm có tổng bằng 39, sau dó ta đặt dấu "+" trước các số của một nhóm và đặt dấu trước các số của nhóm kia.
Chẳng hạn : Một nhóm là (+1, +2, +3, +4, +6, +11, +12), nhóm kia là (-5, -7, -8, -9,-10).
Hoặc một nhóm là (-1, -2, -3, -4, -6, -11, -12), nhóm kia là (+5, +7, +8, +9,+10).
Em hãy tìm thêm các cách khác.
9. Không thể chia hai vế của đẳng thức cho 3b - 2a vì 3b - 2a = 0 do 3b = 2a.
10. Không thể chia hai vế của đẳng thức cho a – b – c vì a- b - c = 0 do a = b + c.