Ôn tập hè Toán 6 bài 4: Các phép tính về phân số. Đoạn thẳng
2020-07-19T09:34:05-04:00
2020-07-19T09:34:05-04:00
https://sachgiai.com/Toan-hoc/on-tap-he-toan-6-bai-4-cac-phep-tinh-ve-phan-so-doan-thang-13407.html
/themes/whitebook/images/no_image.gif
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Chủ nhật - 19/07/2020 09:12
Ôn tập hè Toán 6 bài 4: Các phép tính về phân số. Đoạn thẳng
A. KIẾN THỨC CƠ BẢN
• Số có dạng  với a, b ∈ Z, b ≠ 0 gọi là phân số.
• Hai phân số bằng nhau :
với a, b ∈ Z, b ≠ 0 gọi là phân số.
• Hai phân số bằng nhau :  =
=  ⇔ a . d = b . c (b ≠ 0, d ≠ 0).
• Tính chất cơ bản của phân số:
⇔ a . d = b . c (b ≠ 0, d ≠ 0).
• Tính chất cơ bản của phân số:
 =
= 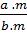 (m ∈ Z, m ≠ 0);
(m ∈ Z, m ≠ 0);
 =
= 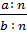 (n ∈ ƯC (a; b))
• Để rút gọn một phân số đen tối giản, ta chia cả tử và mẫu cho ƯCLN của chúng.
• Quy đồng mẫu nhiều phân số với mẫu dương :
- Tìm BCNN của các mẫu ;
- Tìm thừa số phụ của mỗi mẫu ;
- Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
• Các phép tính về phân số
(n ∈ ƯC (a; b))
• Để rút gọn một phân số đen tối giản, ta chia cả tử và mẫu cho ƯCLN của chúng.
• Quy đồng mẫu nhiều phân số với mẫu dương :
- Tìm BCNN của các mẫu ;
- Tìm thừa số phụ của mỗi mẫu ;
- Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
• Các phép tính về phân số

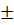
 =
=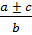 ;
;  +
+  =
= 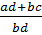 ;
;  -
-  =
=  +
+ 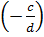
 .
.  =
= 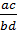 ;
;  :
:  =
=  .
.  =
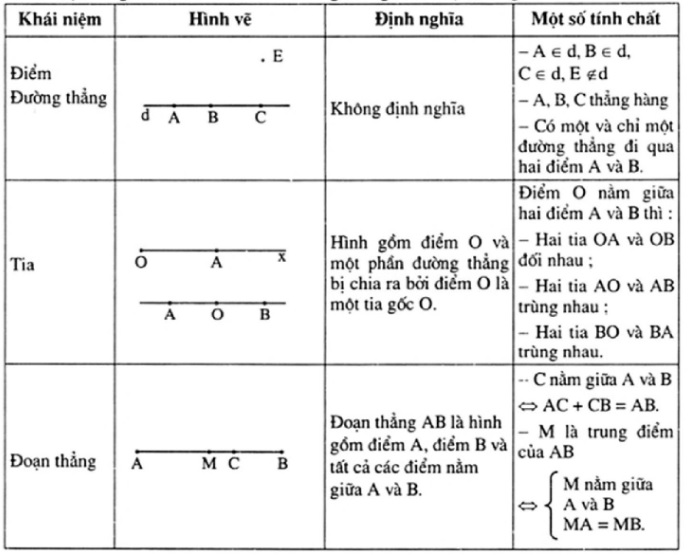
= 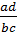 • Hệ thống kiến thức về điểm, đường thẳng, tia, đoạn thẳng.
• Hệ thống kiến thức về điểm, đường thẳng, tia, đoạn thẳng.
 B. MỘT SỐ VÍ DỤ
Ví dụ 1. Cho biểu thức A =
B. MỘT SỐ VÍ DỤ
Ví dụ 1. Cho biểu thức A = 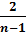 (n ∈ Z).
a) Số nguyên n phải có điều kiện gì để A là phân số ?
b) Tìm tất cả các giá trị nguyên của n để A là số nguyên.
Giải.
a) Ta có 1 ∈ Z, n ∈ Z nên n - 1 ∈ Z. Để A là phân số cần có điều kiện n - 1 ≠ 0 hay n ≠ 1.
b) Để A là số nguyên ta phải có n - 1 là ước của 2.
Ư(2) = { - 2 ; - 1 ; 1 ; 2}. Ta có bảng sau :
(n ∈ Z).
a) Số nguyên n phải có điều kiện gì để A là phân số ?
b) Tìm tất cả các giá trị nguyên của n để A là số nguyên.
Giải.
a) Ta có 1 ∈ Z, n ∈ Z nên n - 1 ∈ Z. Để A là phân số cần có điều kiện n - 1 ≠ 0 hay n ≠ 1.
b) Để A là số nguyên ta phải có n - 1 là ước của 2.
Ư(2) = { - 2 ; - 1 ; 1 ; 2}. Ta có bảng sau :
| n - 1 |
-2 |
-1 |
1 |
2 |
| n |
-1 |
0 |
2 |
3 |
Vây n ∈ {-1; 0; 2; 3).
Ví dụ 2. Lập các cập phân số bằng nhau từ đẳng thức 3.4 = 2.6.
Giải. Từ đẳng thức 3 . 4 = 2 . 6 (1) ta có  =
=  Viết đẳng thức (1) thành 3 . 4 = 6 . 2 ta có
Viết đẳng thức (1) thành 3 . 4 = 6 . 2 ta có  =
=  Viết đẳng thức (1) thành 4 . 3 = 2 . 6 ta có
Viết đẳng thức (1) thành 4 . 3 = 2 . 6 ta có  =
=  Viết đẳng thức (1) thành 4 . 3 = 6 . 2 ta có
Viết đẳng thức (1) thành 4 . 3 = 6 . 2 ta có  =
=  Ví dụ 3. Cho
Ví dụ 3. Cho =
= 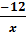 . Tìm số nguyên x theo hai cách
Cách 1. Áp dụng tính chất cơ bản của phân số;
Cách 2. Áp dụng định nghĩa phân số bằng nhau.
Giải.
Cách 1:
. Tìm số nguyên x theo hai cách
Cách 1. Áp dụng tính chất cơ bản của phân số;
Cách 2. Áp dụng định nghĩa phân số bằng nhau.
Giải.
Cách 1:  =
= 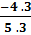 =
= 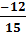 . Do đó ta có
. Do đó ta có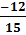 =
= 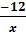 suy ra x = 15
Cách 2 : Từ =
suy ra x = 15
Cách 2 : Từ =  =
= 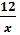 suy ra - 4 . x = 5 . (- 12).
Do đó x=
suy ra - 4 . x = 5 . (- 12).
Do đó x= 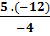 = 15.
Ví dụ 4. Rút gọn các phân số sau :
a)
= 15.
Ví dụ 4. Rút gọn các phân số sau :
a) 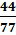 b)
b) 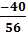 c)
c) 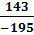 d)
d) 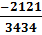 Giải.
a)
Giải.
a) 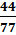 =
=  =
=  b)
b)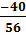 =
= 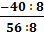 =
= 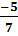 c)
c) 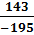 =
= 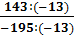 =
= 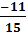 d)
d) 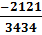 =
= 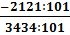 =
= 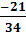 Ví dụ 5. So sánh giá trị của hai biếu thức sau:
A =
Ví dụ 5. So sánh giá trị của hai biếu thức sau:
A =  +
+  :
: 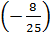 B =
B = 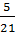 .
. 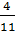 +
+  .
. 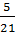 -
-  Giải.
A =
Giải.
A =  +
+  :
: 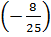 =
=  +
+  .
. 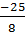 =
=  +
+ 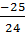 =
= 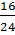 +
+ 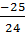 =
= 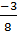 B =
B = 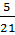 .
. 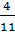 +
+  .
. 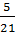 -
-  =
= 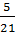 .
.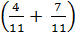 -
- =
= 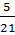 . 1 -
. 1 -  =
= 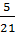 +
+ 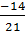 =
= 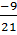 =
= 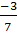 Vì
Vì  =
=  <
<  =
=  nên
nên 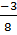 >
> 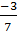 . Vậy A > B
Lưu ý : Khi tính giá trị của biểu thức, cần chú ý thứ tự thực hiện các phép tính và áp dụng tính chất các phép tính.
Khi so sánh hai số âm cần nhớ : số nào có giá trị tuyệt dối nhỏ hơn thì số' dó lớn hơn.
Ví dụ 6. Tính :
a) 3,5 + 4
. Vậy A > B
Lưu ý : Khi tính giá trị của biểu thức, cần chú ý thứ tự thực hiện các phép tính và áp dụng tính chất các phép tính.
Khi so sánh hai số âm cần nhớ : số nào có giá trị tuyệt dối nhỏ hơn thì số' dó lớn hơn.
Ví dụ 6. Tính :
a) 3,5 + 4 ;
b) 8
;
b) 8 - 6,25;
c) 5 - 4
- 6,25;
c) 5 - 4 ;
d) 11
;
d) 11 . 2
Giải.
a) 3,5 + 4
. 2
Giải.
a) 3,5 + 4 = 3
= 3 + 4
+ 4 =
= 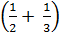 = 7 +
= 7 +  = 7
= 7
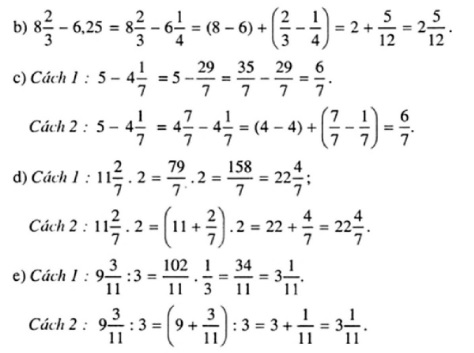 Ví dụ 7. Cho hình 2 :
Ví dụ 7. Cho hình 2 :
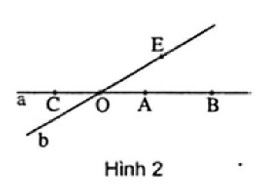 a) Dùng các kí hiệu ∈, ∉ để viết các điểm nằm trên đường thẳng a, các điểm không nằm trên đường thẳng a.
b) Điểm O nằm giữa hai điểm nào ? Điếm A nằm giữa hai điểm nào ?
c) Tìm các điểm nằm cùng phía đối với O.
d) Tìm các điểm nằm khác phía đối với A.
c) Kể tốn các tia gốc O đối nhau, không đối nhau.
g) Kể tên các tia gốc A trùng nhau.
Giải.
a) A ∈ a, B ∈ a, C ∈ a, O ∈ a, E ∉ a.
b) Điểm O nằm giữa c và A, điểm O còn nằm giữa C và B.
Điểm A nằm giữa C và B, điểm A còn nằm giữa O và B.
c) Các điểm A và B nằm cùng phía đối với O.
d) C và B nằm khác phía đối với A ; O và B nằm khác phía đối với A.
e) Các tia gốc O đối nhau là OC và OA, OC và OB.
Các tia gốc O không đối nhau là OE và OC, OE và OA, OE và OB.
g) Các tia gốc A trùng nhau là AO và AC.
Ví dụ 8. Cho bốn điểm M, N, P, Q trong đó ba điểm M. N, p thẳng hàng, ba điểm N, P, Q thẳng hàng. Hỏi bốn điểm M, N, P, Q có thẳng hàng không ? Vì sao ?
a) Dùng các kí hiệu ∈, ∉ để viết các điểm nằm trên đường thẳng a, các điểm không nằm trên đường thẳng a.
b) Điểm O nằm giữa hai điểm nào ? Điếm A nằm giữa hai điểm nào ?
c) Tìm các điểm nằm cùng phía đối với O.
d) Tìm các điểm nằm khác phía đối với A.
c) Kể tốn các tia gốc O đối nhau, không đối nhau.
g) Kể tên các tia gốc A trùng nhau.
Giải.
a) A ∈ a, B ∈ a, C ∈ a, O ∈ a, E ∉ a.
b) Điểm O nằm giữa c và A, điểm O còn nằm giữa C và B.
Điểm A nằm giữa C và B, điểm A còn nằm giữa O và B.
c) Các điểm A và B nằm cùng phía đối với O.
d) C và B nằm khác phía đối với A ; O và B nằm khác phía đối với A.
e) Các tia gốc O đối nhau là OC và OA, OC và OB.
Các tia gốc O không đối nhau là OE và OC, OE và OA, OE và OB.
g) Các tia gốc A trùng nhau là AO và AC.
Ví dụ 8. Cho bốn điểm M, N, P, Q trong đó ba điểm M. N, p thẳng hàng, ba điểm N, P, Q thẳng hàng. Hỏi bốn điểm M, N, P, Q có thẳng hàng không ? Vì sao ?
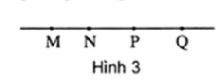 Giải. (h. 3)
Cách 1. Ba điểm M, N, P thẳng hàng nên chúng cùng nằm trôn một đường thẳng d. Ba điểm N, P, Q thẳng hàng nên chúng cùng nằm trên một đường thẳng d'.
Hai đường thẳng d và d' có hai điểm chung là N và P nên chúng phải trùng nhau. Suy ra bốn điểm M, N, P, Q thẳng hàng.
Cách 2. Ba điểm M, N, P thẳng hàng nên M thuộc đường thẳng NP (1).
Ba điểm N, P, Q thẳng hàng nên Q thuộc đường thẳng NP (2).
Từ (1) và (2) suy ra M, Q cùng thuộc đường thẳng NP nghĩa là bốn điểm M, N, P. Q thẳng hàng.
Ví dụ 9. Cho điểm O nằm giữa hai điểm A và B ; điểm M nằm giữa hai điểm A và O ; điểm N nằm giữa hai điểm B và O.
a) Nêu tên các tia trùng nhau gốc O.
b) Chứng tỏ rằng điểm O nằm giữa hai điểm M và N.
Giải. (h. 3)
Cách 1. Ba điểm M, N, P thẳng hàng nên chúng cùng nằm trôn một đường thẳng d. Ba điểm N, P, Q thẳng hàng nên chúng cùng nằm trên một đường thẳng d'.
Hai đường thẳng d và d' có hai điểm chung là N và P nên chúng phải trùng nhau. Suy ra bốn điểm M, N, P, Q thẳng hàng.
Cách 2. Ba điểm M, N, P thẳng hàng nên M thuộc đường thẳng NP (1).
Ba điểm N, P, Q thẳng hàng nên Q thuộc đường thẳng NP (2).
Từ (1) và (2) suy ra M, Q cùng thuộc đường thẳng NP nghĩa là bốn điểm M, N, P. Q thẳng hàng.
Ví dụ 9. Cho điểm O nằm giữa hai điểm A và B ; điểm M nằm giữa hai điểm A và O ; điểm N nằm giữa hai điểm B và O.
a) Nêu tên các tia trùng nhau gốc O.
b) Chứng tỏ rằng điểm O nằm giữa hai điểm M và N.
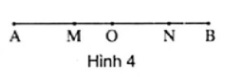 Giải. (h. 4)
a) Điểm M nằm giữa hai điểm A và O nên hai tia OM và OA trùng nhau (1).
Giải. (h. 4)
a) Điểm M nằm giữa hai điểm A và O nên hai tia OM và OA trùng nhau (1).
Điểm N nằm giữa hai điểm B và O nên hai tia ON và OB trùng nhau (2).
b) Điểm O nằm giữa hai điểm A và B nên hai tia OA và OB đối nhau (3).
Từ (1), (2) và (3) suy ra hai tia OM và ON đối nhau, do đó điểm O nằm giữa hai điểm M và N.
Ví dụ 10. Cho đoạn thẳng AB và trung điểm M của nó. Lấy điểm C nằm giữa hai điểm A và M. Chứng tỏ rằng CB = CA + 2CM.
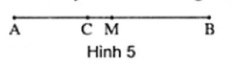 Giải: (h.5)
M là trung điểm của AB nên M nằm giữa A và B. Suy ra hai tia MA và MB đối nhau (1).
C nằm giữa A và M nên hai tia MA và MC trùng nhau (2). Từ (1) và (2) suy ra hai tia MC và MB đối nhau. Do dó M nằm giữa C và B. Ta có CM + MB = CB (3).
C nằm giữa A và M nên CM + CA = AM (4).
Cộng theo từng vế (3) và (4) ta được 2CM + CA + MB = CB + AM (5).
M là trung điểm của AB nên MB = AM (6).
Từ (5) và (6) suy ra CB = CA + 2CM.
C. BÀI TẬP
1. Hãy tìm một phân số có tử số nhỏ hơn mẫu sô, nhưng khi quay 180° theo chiều kim đồng hồ hoặc ngược lại, ta được một phân số mới vẫn bằng phân số cũ.
2. Hãy biểu diễn số 100 bằng 10 chữ số khác nhau (cùng với các phép tính).
3. Hãy tìm các cặp phân số có tính chất : hiệu của hai phân số cũng bằng hiệu các bình phương của hai phân số ấy.
Ví dụ : Cặp phân số
Giải: (h.5)
M là trung điểm của AB nên M nằm giữa A và B. Suy ra hai tia MA và MB đối nhau (1).
C nằm giữa A và M nên hai tia MA và MC trùng nhau (2). Từ (1) và (2) suy ra hai tia MC và MB đối nhau. Do dó M nằm giữa C và B. Ta có CM + MB = CB (3).
C nằm giữa A và M nên CM + CA = AM (4).
Cộng theo từng vế (3) và (4) ta được 2CM + CA + MB = CB + AM (5).
M là trung điểm của AB nên MB = AM (6).
Từ (5) và (6) suy ra CB = CA + 2CM.
C. BÀI TẬP
1. Hãy tìm một phân số có tử số nhỏ hơn mẫu sô, nhưng khi quay 180° theo chiều kim đồng hồ hoặc ngược lại, ta được một phân số mới vẫn bằng phân số cũ.
2. Hãy biểu diễn số 100 bằng 10 chữ số khác nhau (cùng với các phép tính).
3. Hãy tìm các cặp phân số có tính chất : hiệu của hai phân số cũng bằng hiệu các bình phương của hai phân số ấy.
Ví dụ : Cặp phân số  và
và  có
có  -
-  =
=  và
và 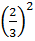 -
- 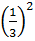 =
=  -
-  =
=  =
=  4. Đố vui: Thầy giáo ghi lên bảng bốn số 3 ; 6 ; 9 ; 12 và tổ chức cho cả lớp chơi trò chơi "Tính trung bình cộng của 3 số" như sau : Lần lượt từng bạn lên viết 4 số mà mỗi số là trung bình cộng của 3 trong 4 số vừa được viết trên bảng.
Bạn đầu tiên viết các số 9 ; 8 ; 7 ; 6.
Bạn thứ hai viết các số 7 ;
4. Đố vui: Thầy giáo ghi lên bảng bốn số 3 ; 6 ; 9 ; 12 và tổ chức cho cả lớp chơi trò chơi "Tính trung bình cộng của 3 số" như sau : Lần lượt từng bạn lên viết 4 số mà mỗi số là trung bình cộng của 3 trong 4 số vừa được viết trên bảng.
Bạn đầu tiên viết các số 9 ; 8 ; 7 ; 6.
Bạn thứ hai viết các số 7 ; 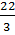 ;
; 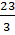 ; 8.
Ai cũng tính rất giỏi và dược thầy khen đúng.
Đến lượt bạn Tuấn vừa ghi xong 4 số ;
; 8.
Ai cũng tính rất giỏi và dược thầy khen đúng.
Đến lượt bạn Tuấn vừa ghi xong 4 số ; 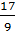 ;
; 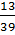 ; 10 ;
; 10 ; 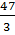 dù "bị" thầy nói ngay là sai.
Đố em biết có cách nào kiểm tra nhanh kết quả.
5. Vì sao chi cần đánh lưới hai lần là có thể ước đoán trong ao có bao nhiêu cá ? Để ước lượng trong một ao nuôi cá có bao nhiêu cá, em có thể làm như sau : Trước hết, em dùng một cái lưới có cỡ mắt nhất định rồi quăng xuống ao. Một lát sau kéo lưới lên, già sử lần đầu đánh được 30 con, em hãy đánh dấu từng con một rồi thả tất cả xuống ao. Lại đánh lần thứ hai, giả sử đánh được 40 con và trong số đó có hai con có đánh dấu. Lúc ấy chit cần tính toán đơn giản, em cũng có thể biết được trong ao có khoảng bao nhiêu con cá.
Em có biết vì sao không ?
6. Kết quả của phép nhân 5 .
dù "bị" thầy nói ngay là sai.
Đố em biết có cách nào kiểm tra nhanh kết quả.
5. Vì sao chi cần đánh lưới hai lần là có thể ước đoán trong ao có bao nhiêu cá ? Để ước lượng trong một ao nuôi cá có bao nhiêu cá, em có thể làm như sau : Trước hết, em dùng một cái lưới có cỡ mắt nhất định rồi quăng xuống ao. Một lát sau kéo lưới lên, già sử lần đầu đánh được 30 con, em hãy đánh dấu từng con một rồi thả tất cả xuống ao. Lại đánh lần thứ hai, giả sử đánh được 40 con và trong số đó có hai con có đánh dấu. Lúc ấy chit cần tính toán đơn giản, em cũng có thể biết được trong ao có khoảng bao nhiêu con cá.
Em có biết vì sao không ?
6. Kết quả của phép nhân 5 .  là :
(A)
là :
(A) 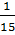 ; (B)
; (B)  ; (C)
; (C) 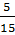 ; (D)
; (D) 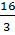 Hãy chọn phương án đúng.
7. Giá trị của biểu thức
Hãy chọn phương án đúng.
7. Giá trị của biểu thức  +
+  .
. 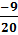 là:
(A)
là:
(A) 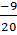 ; (B)
; (B)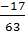 ; (C)
; (C) 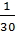 ; (D)
; (D) 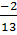 8. Tính giá trị của mỗi biểu thức sau:
A =
8. Tính giá trị của mỗi biểu thức sau:
A =  . 0,25 : (0,25 :
. 0,25 : (0,25 :  )
B =
)
B = 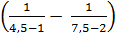 :
: 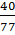 9. Hãy tìm cách trồng 9 cây thành 8 hàng, mỗi hàng 3 cây và vẽ hình để thể hiện điều đó.
10. Vẽ hai tia chung gốc và không đối nhau Ox, Oy. Trên tia Ox lấy hai điểm A và B (điểm A nằm giữa O và B). Trên tia Oy lấy hai điểm M và N sao cho OM = OA. ON = OB.
a) Chứng tỏ rằng điểm M năm giữa O và N.
b) So sánh AB với MN.
c) Lấy C là một điểm nằm giữa O và B (C không trùng A). Biết OC = AB, hãy so sánh OA với BC.
9. Hãy tìm cách trồng 9 cây thành 8 hàng, mỗi hàng 3 cây và vẽ hình để thể hiện điều đó.
10. Vẽ hai tia chung gốc và không đối nhau Ox, Oy. Trên tia Ox lấy hai điểm A và B (điểm A nằm giữa O và B). Trên tia Oy lấy hai điểm M và N sao cho OM = OA. ON = OB.
a) Chứng tỏ rằng điểm M năm giữa O và N.
b) So sánh AB với MN.
c) Lấy C là một điểm nằm giữa O và B (C không trùng A). Biết OC = AB, hãy so sánh OA với BC.
HƯỚNG DẪN GIẢI
1. Phân số  2. Cách 1:
2. Cách 1:  + 49 + 50 +
+ 49 + 50 + 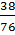 = 100
Cách 2: 5 + 24 + 70 +
= 100
Cách 2: 5 + 24 + 70 + 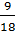 +
+  = 100
Cách 3: 19 + 80 +
= 100
Cách 3: 19 + 80 +  +
+ 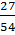 = 100
Cách 4: 3 + 9 + 87 +
= 100
Cách 4: 3 + 9 + 87 +  +
+ 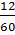 = 100
3. Có vô số cặp phân số thoả mãn yêu cầu của đầu bài. Đó là những cặp phân số bằng nhau và những cặp phân số có tổng bằng 1. Bạn hãy giải thích vì sao.
Chẳng hạn : cặp
= 100
3. Có vô số cặp phân số thoả mãn yêu cầu của đầu bài. Đó là những cặp phân số bằng nhau và những cặp phân số có tổng bằng 1. Bạn hãy giải thích vì sao.
Chẳng hạn : cặp  và
và  , cặp
, cặp  và
và 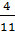 , cặp
, cặp  và
và  4. Giả sử cho trước 4 số a, b. c, d.
Nếu tính trung bình cộng của 3 số bất kì trong 4 số trên thì ta có 4 số trung bình cộng sau
4. Giả sử cho trước 4 số a, b. c, d.
Nếu tính trung bình cộng của 3 số bất kì trong 4 số trên thì ta có 4 số trung bình cộng sau 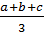 ,
, 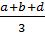 ,
, 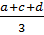 ,
, 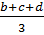 Tổng của 4 số trung bình cộng là :
Tổng của 4 số trung bình cộng là :
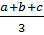 +
+ 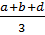 +
+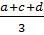 +
+ 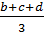 =
= 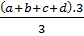 = a + b + c + d
Do đó, tổng của 4 số ở bất kì lần viết nào cũng bằng tổng của 4 số ban đầu và
là 3 + 6 + 9 + 12 = 30. Tông của 4 số bạn Tuấn viết là
= a + b + c + d
Do đó, tổng của 4 số ở bất kì lần viết nào cũng bằng tổng của 4 số ban đầu và
là 3 + 6 + 9 + 12 = 30. Tông của 4 số bạn Tuấn viết là
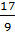 +
+ 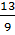 + 10 +
+ 10 + 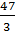 = 29
Như vậy, bạn Tuấn chắc chắn đã tính sai.
(Theo Nguyễn Đức Tấn. "Ảo thuật và đố vui toán học". NXB Giáo dục - 2004).
5. Số cá có đánh dấu bắt được lần thứ hai chiếm
= 29
Như vậy, bạn Tuấn chắc chắn đã tính sai.
(Theo Nguyễn Đức Tấn. "Ảo thuật và đố vui toán học". NXB Giáo dục - 2004).
5. Số cá có đánh dấu bắt được lần thứ hai chiếm 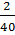 =
= 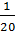 số cá bắt được. Giả sử số cá có đánh dấu được phân bố đều toàn bộ số cá trong ao là n con thì 30 con cá có đánh dấu cũng phải chiếm
số cá bắt được. Giả sử số cá có đánh dấu được phân bố đều toàn bộ số cá trong ao là n con thì 30 con cá có đánh dấu cũng phải chiếm 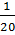 toàn bộ số cá n (con) tức là
toàn bộ số cá n (con) tức là  ≈
≈ 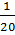 . Do đó n ≈ 30. 20 = 600 (con).
N chỉ là một số gần đúng vì chưa tính số cá nhỏ hơn mắt lưới, mắt lưới càng nhỏ thì số cá ước đoán càng chính xác.
(theo Dương Vinh Tường và các tác giả khác, “Mười vạn câu hỏi phần toán – tập 2”. NXB Khoa học - 1964)
6. Chọn B
7. Chọn C
8. A =
. Do đó n ≈ 30. 20 = 600 (con).
N chỉ là một số gần đúng vì chưa tính số cá nhỏ hơn mắt lưới, mắt lưới càng nhỏ thì số cá ước đoán càng chính xác.
(theo Dương Vinh Tường và các tác giả khác, “Mười vạn câu hỏi phần toán – tập 2”. NXB Khoa học - 1964)
6. Chọn B
7. Chọn C
8. A =  .
.  :
: 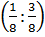 =
= 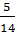 :
:  =
= 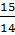 =
= 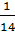 B =
B = 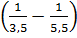 :
: 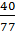 =
= 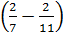 .
.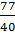 =
=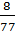 .
.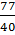 =
=  9. h.10
9. h.10
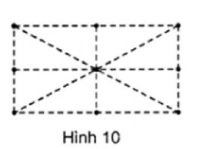 10. h. 11
10. h. 11
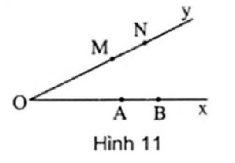 a) A nằm giữa O và B nên OA < OB mà OM = OA, ON = OB
nên OM < ON. Hai điểm M. N cùng thuộc tia Oy suy ra M nằm giữa O và N.
b) Ta có OA + AB = OB. (1)
Ta lại có OA = OM. OB = ON nên từ (1) và (2) suy ra AB = MN.
c) A nằm giữa O và B nên OA + AB = OB (1)
C nằm giữa O và B nên OC + CB = OB (2)
Từ (1) và (2) suy ra : OA + AB = OC + CB ( = OB) (3)
Trong đẳng thức (3) ta có OC = AB suy ra OA = CB.
a) A nằm giữa O và B nên OA < OB mà OM = OA, ON = OB
nên OM < ON. Hai điểm M. N cùng thuộc tia Oy suy ra M nằm giữa O và N.
b) Ta có OA + AB = OB. (1)
Ta lại có OA = OM. OB = ON nên từ (1) và (2) suy ra AB = MN.
c) A nằm giữa O và B nên OA + AB = OB (1)
C nằm giữa O và B nên OC + CB = OB (2)
Từ (1) và (2) suy ra : OA + AB = OC + CB ( = OB) (3)
Trong đẳng thức (3) ta có OC = AB suy ra OA = CB.
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.