1. Định nghĩa đường trung bình của tam giác
Câu hỏi trang 81: Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
 Giải:
Giải:
Quan sát Hình 4.14, ta thấy:
* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
* Xét ∆IHK có:
• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆IHK.
• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆IHK.
• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆IHK.
Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.
2. Tính chất đường trung bình của tam giác
Hoạt động 1 trang 82: Cho DE là đường trung bình của tam giác ABC (H.4.15).Sử dụng định lí Thales đảo, chứng minh rằng DE // BC
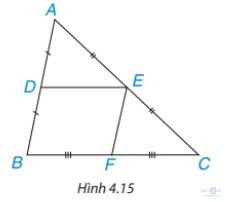 Giải:
Giải:
Ta có DE là đường trung bình của tam giác ABC nên:
• D là trung điểm của AB hay AD =

AB nên
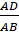
=

• E là trung điểm của AC hay AE =

AC nên
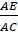
=

Xét tam giác ABC có
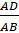
=
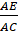
=

, theo định lí Thales đảo, ta suy ra DE // BC (đpcm).
Hoạt động 2 trang 82: Cho DE là đường trung bình của tam giác ABC (H.4.15). Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra DE = 
BC
 Giải:
Giải:
Ta có: F là trung điểm của BC nên CF =

BC, suy ra
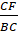
=
12
Mà E là trung điểm của AC nên CE =

CA, suy ra
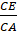
=
12
Do đó trong DABC có
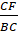
=
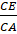
=

, theo định lí Thales đảo ta có: EF // AB.
Xét tứ giác DEFB có DE // BF (vì DE // BC, theo HĐ1); EF // BD (vì EF // AB)
Do đó tứ giác DEFB là hình bình hành.
Suy ra DE = BF mà BF =

BC nên DE =

BC
Luyện tập trang 83: Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?
Giải:

Tam giác ABC cân tại A nên
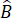
=
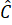
Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.
Suy ra DE // BC nên tứ giác DECB là hình thang.
Hình thang DECB có
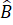
=
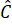
nên là hình thang cân.
3. Giải bài tập trang 83
Bài 4.6: Tính các độ dài x, y trong Hình 4.18.
 Giải:
Giải:
• Hình 4.18a)
Ta có: DH = HF, H ∈ DF nên H là trung điểm của DF;
EK = KF, K ∈ EF nên K là trung điểm của EF.
Xét tam giác DEF có H, K lần lượt là trung điểm của DF, EF nên HK là đường trung bình của tam giác DEF.
Suy ra HK =

DE =
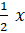
Do đó x = 2HK = 2 . 3 = 6.
• Hình 4.18b)
Vì MN ⊥ AB, AC ⊥ AB nên MN // AC.
Mà M là trung điểm của AB (vì AM = BM = 3)
Suy ra MN là đường trung bình của tam giác ABC.
Do đó N là trung điểm của BC nên y = NC = BN = 5.
Vậy x = 6; y = 5.
Bài 4.7: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang
b) Tứ giác MNPB là hình gì? Tại sao?
Giải:

a) Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra MN // BC.
Tứ giác BMNC có MN // BC nên tứ giác BMNC là hình thang (đpcm).
b) Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP // AB hay NP // MB.
Tứ giác MNPB có MN // BP (do MN // BC); BM // NP (chứng minh trên).
Do đó, tứ giác MNPB là hình bình hành.
Bài 4.8: Cho tam giác ABC có trung tuyến AM. Lấy hai điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E
a) Chứng minh DC // EM
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM
Giải:

a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.
Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.
Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.
Do đó DC // EM (tính chất đường trung bình).
b) Ta có D là trung điểm của AE (vì AD = DE, D ∈ AE).
Mà DI // EM (vì DC // EM).
Do đó DI là đường trung bình của tam giác AEM.
Suy ra I là trung điểm của AM.
Bài 4.9: Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh rằng tứ giác AHOK là hình chữ nhật
Giải:

Vì ABCD là hình chữ nhật nên
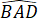
= 90
o và hai đường chéo AC, BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.
Suy ra AB ⊥ AD; O là trung điểm của AC và BD.
Vì O, H lần lượt là trung điểm của BD và AB nên OH là đường trung bình của tam giác ABD.
Suy ra OH // AD mà AB ⊥ AD nên OH ⊥ AB hay
AHO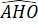
= 90
o
Tương tự, ta chứng minh được: OK ⊥ AD hay
AKO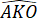
= 360°
Ta có:
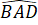
+
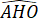
+
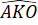
+
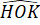
= 360
o
90° + 90° + 90° +
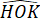
= 360°
270
o +
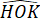
= 360°
Suy ra
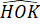
= 360° - 270
o = 90
o
Tứ giác AHOK có

= 90
o;
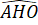
= 90
o ;
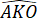
= 90
o ;
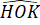
= 90
o
Do đó, tứ giác AHOK là hình chữ nhật.