Trắc nghiệm (3 điểm)
Câu 1: Chọn kết quả sai:
A. 4x(2x2 – 5x + 3) = 8x3 – 20x2 + 12x
B. 5x(3x2 – 6x – 1) = 15x3 – 30x2 – 5x
C. (–2x)( –3x2 + 4x –7) = –6x3 – 8x2 + 14x
D. (–3x)( –x2 – 3x – 4) = 3x3 + 9x2 + 12x
Câu 2: Giá trị của biểu thức x2 – 4xy + 4y2 tại x = 99 và y = 1/2 là:
A. 9604 B. 9801 C. 10000 D. 10201
Câu 3: Đẳng thức nào sau đây không đúng?
A. x2 – 6x + 9 = (x – 3)2
B. x2 – 6x + 9 = (3 – x)2
C. x2 – 6x + 9 = –(3 – x)2
Câu 4: Phân tích đa thức x2 – y2 – 2y – 1 thành nhân tử là:
A. (x + y)(x – y)(y – 1)
B. (x + y)(x – y)(y + 1)
C. (x + y + 1)(x + y – 1)
D. (x + y + 1)(x – y – 1)
Câu 5: Biết a + b = –7 và ab = 12. Giá trị của biểu thức a3 + b3 là:
A. 91 B. –91 C. 84 D. –84
Câu 6: Kết quả của phép chia (10x2 + 23x – 5) : (2x + 5) là:
A. 5x – 1 B. 5x + 1
C. 5x – 5 D. 5x + 5
Tự luận (7 điểm)
Bài 1: (1,5 điểm) Thực hiện các phép tính:
a) (x2 – 3x)(3x2 – x + 4)
b) (6x3 – x2 – 14x + 3) : (2x – 3)
Bài 2: (2 điểm)
a) Rút gọn các biểu thức:
i) (x2 – 5) – (x + 7)(x – 7)
ii) (5x + 1)2 + (5x – 1)2 + 2(5x + 1)(5x – 1)
b) Tìm giá trị nhỏ nhất của biểu thức:
P = x2 + y2 – 2x + 6y + 12
Bài 3: (2 điểm) Phân tích các đa thức sau thành nhân tử:
a) x3 + 4x2 – 2x – 8
b) 4x2 – 25 + (2x + 5)2
Bài 4: (1,5 điểm)
a) Tìm x biết (x + 3)2 = (x + 3)(x – 3)
b) Chứng tỏ A = (x + 1)(x +2)(x + 3)(x + 4) – 24 chia hết cho x (với x ≠ 0)
ĐÁP ÁN
Trắc nghiệm (3 điểm)
Câu 1: C Câu 4: D
Câu 2: C Câu 5: B
Câu 3: B Câu 6: A
Tự luận (7 điểm)
Bài 1: (1,5 điểm) Thực hiện các phép tính:
a) (x2 – 3x)(3x2 – x + 4)
= 3x4 - x3 + 4x2 - 9x3 + 3x2 -12x
= 3x4 - 10x3 + 7x2 - 12x
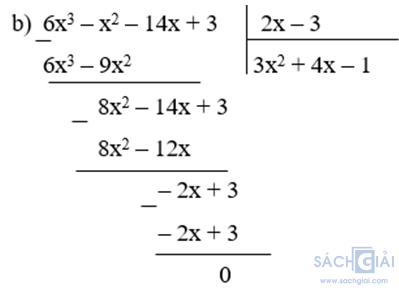
Vậy (6x3 – x2 – 14x + 3) : (2x – 3) = 3x2 + 4x – 1
Bài 2: (2 điểm)
a) Rút gọn các biểu thức:
i) (x2 – 5) – (x + 7)(x – 7)
= (x2 - 5) - (x2 - 49)
= x2 - 5 - x2 + 49 = 44
ii) (5x + 1)2 + (5x – 1)2 + 2(5x + 1)(5x – 1)
= [(5x + 1) + (5x - 1)]2
= (10x)2 = 100x2
b) Ta có: P = (x – 1)2 + (y + 3)2 + 2 ≥ 2 vì (x – 1)2 ≥ 0; (y + 3)2 ≥ 0, với mọi x, y
Vậy giá trị nhỏ nhất của P bằng 2
Dấu “=” xảy ra khi x – 1 = 0 và y + 3 = 0 ⇒ x = 1 và y = -3
Bài 3: (2 điểm) Phân tích các đa thức sau thành nhân tử:
a) x3 + 4x2 – 2x – 8
= (x3 + 4x2) - (2x + 8)
= x2(x + 4) - 2(x + 4)
= (x + 4)(x2 - 2)
= (x + 4)(x + √2)(x - √2)
b) 4x2 - 25 + (2x + 5)2
= (2x + 5)(2x - 5) + (2x + 5)2
= (2x + 5)(2x - 5 + 2x + 5)
= 4x(2x + 5)
Bài 4: (1,5 điểm)
a) Tìm x
(x + 3)2 = (x + 3)(x – 3)
⇔ (x + 3)2 - (x + 3)(x - 3) = 0
⇔ (x + 3)(x + 3 - x + 3) = 0
⇔ 6(x + 3) = 0
⇔ x = -3
Vậy: x = -3
b) Ta có A = (x + 1)(x + 2)(x + 3)(x + 4) – 24
= (x + 1)(x + 4)(x + 2)(x + 3) - 24
= (x2 + 5x + 4)(x2 + 5x + 6) - 24(*)
Đặt x2 + 5x + 5 = t
Thay x2 + 5x + 5 = t vào (*) ta được:
A = (t - 1)(t + 1) - 24
= t2 - 25
= (t - 25)(t + 25)
= (x2 + 5x + 5 + 5)(x2 + 5x + 5 - 5)
= (x2 + 5x + 10)(x2 + 5x)
(x2 + 5x + 10).x(x + 5) chia hết cho x (Với x ≠ 0)
Vậy: A chia hết cho x (Với x ≠ 0)