Phần trắc nghiệm (3 điểm)
Câu 1: Trong các hàm số sau hàm số nào nghịch biến?
A. y = x - 3 B.y = 1/3 x - 1
C. y = √2 - (1 - x) D.y = 5 - (2x + 1)
Câu 2: Giá trị của k để hàm số y = (1 - 3k)x - 3 đồng biến trên R khi:
A.k < 1/3 B.k > 1/3 C.k < -3 D.k > -3
Câu 3: Chọn khẳng định đúng.
A. Đường thẳng x = m (m ≠ 0) thì song song với trục hoành.
B. Đường thẳng y = n (n ≠ 0) thì song song với trục tung.
C. Đường thẳng x = m (m ≠ 0) thì song song với trục tung.
D. Đường thẳng y = 3x - 3 đi qua A(1; 1).
Câu 4: Cho các đường thẳng: (I) y = 3x - 1; (II) y = -3x - 1
(III) y = -3x + 2; (IV) y = 1/3 x - 1
Các cặp đường thẳng song song với nhau trong các đường thẳng trên là:
A.(I) và (III) B.(II) và (III)
C.(I) và (IV) D.(II) và (IV)
Câu 5: Đường thẳng y = √3x + 5 tạo với chiều dương của trục Ox một góc:
A. 60o B.120o C.30o D.90o
Câu 6: Đường thẳng y = ax + b đi qua hai điểm A(0;-3) và B(2; 1/3) là:

Phần tự luận (7 điểm)
Bài 1. (3 điểm)
1) Tìm tọa độ giao điểm của hai đường thẳng (d): y = x và (d’):y = -x + 3.
2) Cho hàm số y = (2 - k)x + k - 1 có đồ thị (d)
a) Với giá trị nào của k thì (d) tạo với Ox một góc tù
b) Tìm k để đường thẳng (d) cắt trục tung tại điểm có hoành độ bằng 5
Bài 2. (3 điểm) Cho đường thẳng (d): y = - x + 1
a) Vẽ đồ thị (d).
b) Trên mặt phẳng tọa độ Oxy lấy điểm M(0;-1). Tính khoảng cách từ điểm M đến đường thẳng (d).
c) Tính diện tích tam giác MAB.
Bài 3. (1 điểm)
Cho hàm số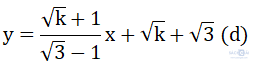
Chứng minh rằng với mọi k ≥ 0, các đường thẳng (d) luôn đi qua một điểm cố định. Xác định tọa độ điểm cố định đó
GIẢI
Phần trắc nghiệm (3 điểm)
Phần tự luận (7 điểm)
Bài 1.
1) Tọa độ giao điểm của (d) và (d') là nghiệm của hệ phương trình:
Cho hàm số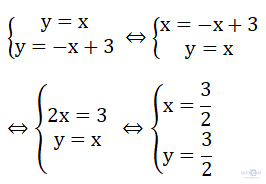
Vậy tọa độ giao điểm của (d) và (d') là (3/2; 3/2)
2) Cho hàm số y = (2 - k)x + k - 1 có đồ thị (d)
a) (d) tạo Ox một góc tù khi và chỉ khi:
2 - k < 0 ⇒ k > 2
b) (d) cắt trục hoành tại điểm có hoành độ bằng 5 khi
0 = (2 - k).5 + k - 1 ⇒ 9 - 4k = 0 ⇒ k = 9/4
Bài 2.
a) Vẽ đồ thị hàm số y = - x + 1 (d)
Cho x = 0 thì y = 1 ta được điểm A(0; 1)
Cho y = 0 thì - x + 1 = 0 ⇒ x = 1 ta được điểm B(1;0)
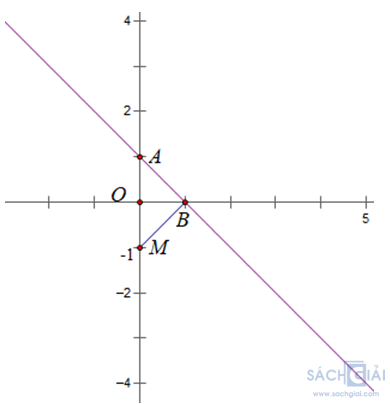
Đường thẳng AB là đồ thị của hàm số y = -x + 1
b) Xét tam giác OMB vuông tại O có:
BM2 = OM2 + OB2 = 1 + 1 = 2 ⇒ BM = √2
Tương tự tam giác OAB vuông tại O có:
BA2 = OA2 + OB2 = 1 + 1 = 2 ⇒ BA = √2
Xét tam giác MAB có:
BM2 + BA2 = 2 + 2 = 4 = AM2
⇒ ΔMAB vuông tại B
Do đó, khoảng cách từ M đến đường thẳng (d) là độ dài đoạn BM = √2
C) Diện tích tam giác MAB là:
SMAB = 1/2 MB.AB = 1/2.√2.√2 = 1 (đơn vị diện tích)
Bài 3. Với k ≥ 0 ta có:
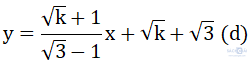
Giả sử (xo; yo) là điểm cố định mà (d) luôn đi qua
Khi đó ta có:
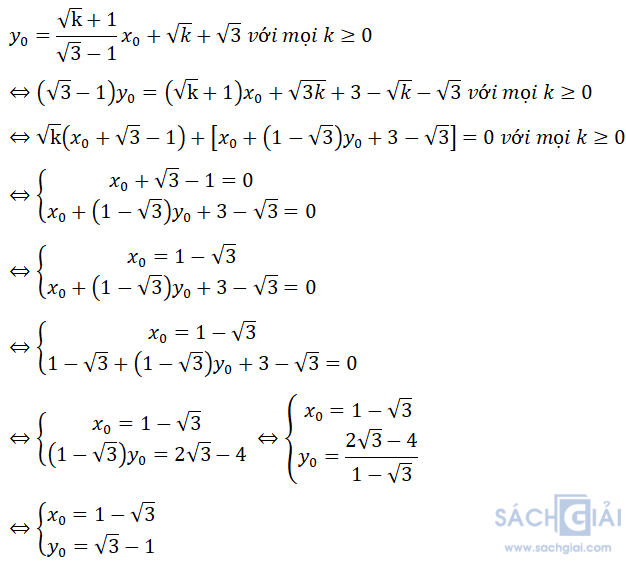
Vậy điểm cố định mà (d) luôn đi qua với mọi k ≥ 0 là (1-√3; √3-1)