Trắc nghiệm (3 điểm)
Câu 1: Chọn kết quả đúng:
Trong tứ giác MNPQ có: ∠M + ∠N + ∠P + ∠Q =?
A. 90o B. 180o C. 360o D. 540o
Câu 2: Cho hình thang ABCD (AB // CD), biết độ dài hai đáy AB = 10cm và CD = 22cm. Gọi H, K lần lượt là trung điểm của AD và BC. Độ dài đoạn thẳng HK là:
A. 16cm B. 8cm C. 11cm D. 32cm
Câu 3: Chọn câu có khẳng định sai:
A. Tứ giác có các cạnh đối song song là hình bình hành.
B. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
C. Hình thang là một hình bình hành.
D. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Câu 4: Chọn câu có khẳng định đúng.
A. Trong tam giác cân, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
B. Trong tam giác vuông, đường cao ứng với cạnh huyền bằng nửa cạnh huyền.
C. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1/3 cạnh huyền.
D. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền.
Câu 5: Cho ΔABC vuông tại A, đường cao AH. Gọi K và M lần lượt là hình chiếu của H trên AB và AC. Gọi N là trung điểm của CH. Số đo góc ∠KMN là:
A. 30o B. 60o C. 90o D. 120o
Câu 6: Cho hình thoi ABCD có ∠A = 60o . Trên cạnh AD lấy điểm H và trên cạnh CD lấy điểm K sao cho AH = DK. Số đo góc ∠HBK là:
A. 30o B. 60o C. 45o D. 90o
Phần tự luận (7 điểm)
Bài 1: (3 điểm) Cho hình thoi ABCD có O là giao điểm hai đường chéo. Gọi I là trung điểm cạnh BC và E là điểm đối xứng với O qua I.
a) Tứ giác OBEC là hình gì? Tại sao?
b) Chứng tỏ E đối xứng với A qua trung điểm J của đoạn OB.
Bài 2: (4 điểm) Cho tm giác ABC vuông tại A ( AB < AC). Gọi I là trung điểm của BC. Qua I vẽ IM ⊥ AB tại M, và IN ⊥ AC tại N.
a) Chứng minh AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh ADCI là hình thoi.
c) Đường thẳng BN cắt DC tại K. Chứng minh:
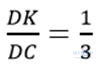
ĐÁP ÁN
Trắc nghiệm
Câu 1: C
Câu 2: A
Câu 3: C
Câu 4: D
Câu 5: C
Câu 6: B
Tự luận (7 điểm)
Bài 1
a) Ta có IB = IC (gt), IO = IE (tính chất đối xứng)
⇒ OBEC là hình bình hành.
Lại có ∠BOC = 90o (tính chất hai đường chéo hình thoi).
Do đó OBEC là hình chữ nhật.
b)Ta có OA = OC (tính chất đường chéo hình thoi)
Mà OC = BE và OC // BE (cmt) nên OA = BE và OA // BE.
Do đó ABEO là hình bình hành
Ta có J là trung điểm của OB nên đường chéo thứ hai AI phải qua J và JA = JE.
⇒ E đối xứng với A qua trung điểm J của đoạn OB.
Bài 2
a) Xét tứ giác ANIM có:
(AMI) = 90o
(ANI) = 90o
(MAN) = 90o
⇒ Tứ giác ANIM là hình chữ nhật (có ba góc vuông)
b) I là trung điểm của BC nên AI là đường trung tuyến của tam giác vuông ABC
⇒ AI = IC = BC/2. (1)
Do đó ΔAIC cân có IN là đường cao nên đồng thời là trung tuyến hay NA = NC (2)
lại có NI = NI (tính chất đối xứng) (3)
Từ (1), (2), (3) ⇒ ADIC là hình thoi.
c) Kẻ qua I đường thẳng song song với BK cắt CD tai E.
Ta có: I là trung điểm của BC; IE // BK
⇒ E là trung điểm của CK hay EK = EC (1)
Mặt khác N là trung điểm của ID và NK // IE ( IE // BK)
⇒ K là trung điểm của DE hay EK = DK (2)