Bài 1 Cho tứ giác ABCD. Gọi E, F theo thứ tự là trung điểm của AB và CD; M, N, P, Q lầ lượt là trung điểm của các đoạn thẳng AF, CE, BF và DE. Gọi I là giao điểm của MP và EF. Chứng minh rằng:
a) I là trung điểm của MP
b) MNPQ là hình bình hành
ĐÁP ÁN
Bài 1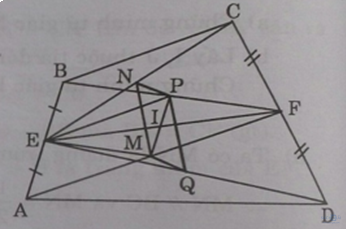
a) Xét tam giác ABF có:E là trung điểm của AB
P là trung điểm của BF
⇒ EP là đường trung bình của ΔABF
⇒ EP // AF và EP = AF/2
M là trung điểm AF (gt)
⇒ MF = AF/2
Do đó EP // MF và EP = MF. Vậy EPFM là hình bình hành
I là giao điểm của hai đường chéo MP và EF nên I là trung điểm của MP.
b) Do tứ giác EPFM là hình bình hành nên I là trung điểm của EF.Chứng minh tương tự ta có ENFQ là hình bình hành mà I là trung điểm của EF ⇒ I là trung điểm của NQ (2)
Từ (1) và (2) ⇒ MNPQ là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).