I. Trắc nghiệm (2 điểm)
Câu 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn:
A. 2x2 - 3x + 1 = 0 B.-2x = 4
C. 2x + 3y = 7 D. 1/x + y = 3
Câu 2: Hệ phương trình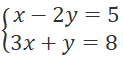 
có nghiệm là:
A. (-3; -1) B. (3; 1)
C. (3; -1) D. (1; -3)
Câu 3: Cho AB là dây cung của đường tròn (O; 4 cm), biết AB = 4 cm, số đo của cung nhỏ AB là:
A. 60o B. 120o C. 30o D. 90o
Câu 4: Bán kính hình tròn nội tiếp hình vuông cạnh 2 cm là:
A.2 cm B.√2 cm C.1 cm D.4 cm
II. Tự luận (8 điểm)
Bài 1 (1, 5 điểm) giải phương trình và hệ phương trình sau:
a) x2 - 7x + 5 = 0
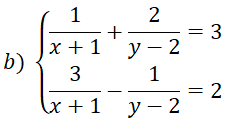
Bài 2 (1, 5 điểm) Cho hai hàm số : y = x2 (P) và y = - x + 2 (d)
a) Vẽ 2 đồ thì hàm số trên cùng 1 hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (d)
c) Viết phương trình đường thẳng d' song song với d và cắt (P) tại điểm có hoành độ -1.
Bài 3 (1, 5 điểm) Cho phương trình x2 + (m – 2)x – m + 1 =0
a) Tìm m để phương trình có 1 nghiệm x = 2. Tìm nghiệm còn lại
b) Chứng minh rằng phương trình luôn có nghiệm với mọi m
c) Tìm giá trị nhỏ nhất của biểu thức A = x12 + x22 -6x1 x2
Bài 4 (3,5 điểm) Cho (O;OA), dây BC vuông góc với OA tại K. Kẻ tiếp tuyến của (O) tại B và A, hai tiếp tuyến này cắt nhau tại H
a) Chứng minh tứ giác OBHA nội tiếp được đường tròn
b) Lấy trên O điểm M (M khác phía với A so với dây BC, dây BM lớn hơn dây MC). Tia MA và BH cắt nhau tại N. chứng minh ∠(NMC) = ∠(BAH)
c) Tia MC và BA cắt nhau tại D. Chứng minh tứ giác MBND nội tiếp được đường tròn.
d) Chứng minh OA ⊥ ND
Hướng dẫn giải
Trắc nghiệm (2 điểm)
Câu 4: Chọn đáp án B
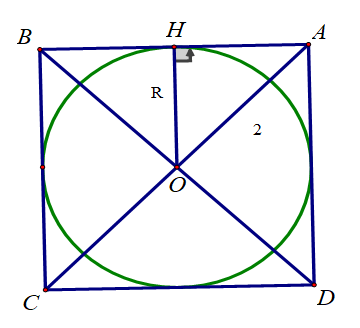
Kẻ OH ⊥ AB. Do ABCD là hình vuông nên ∠OAH = 45o
Xét tam giác OAH vuông tại H có: OH = OA. sin (OAH) = 2.sin 45o =√2
Vậy bán kính đường tròn nội tiếp hình vuông bán kính 2cm là √2 cm
Tự luận (8 điểm)
Bài 1
a) x2 - 7x + 5 = 0
Δ = 72 - 4.1.5 = 49 - 20 = 29 > 0
⇒ Phương trình đã cho có 2 nghiệm phân biệt
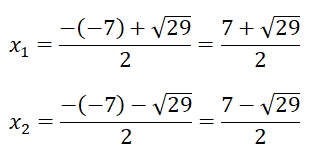
Vậy hệ phương trình đã cho có tập nghiệm
Vậy hệ phương trình đã cho có nghiệm (x; y) = (0; 3)
Bài 2
a) Xét hàm số: y = x2 (P)
Tập xác định R
Bảng giá trị
| x | - 2 | - 1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 2 |
Đồ thị hàm số y = x2 là đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
Xét hàm số: y = - x + 2 (d)
Tập xác định R
Bảng giá trị
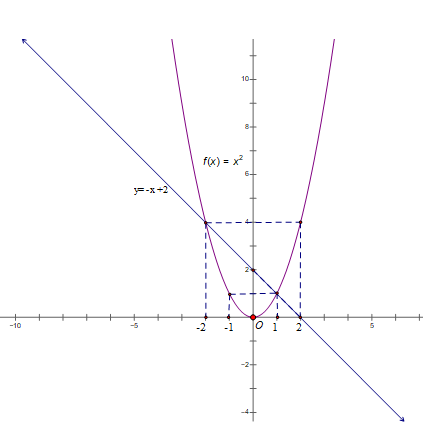
b) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = -x + 2 ⇔ x2 + x - 2 = 0
⇒ Phương trình có nghiệm 1 và -2 ( phương trình dạng a + b + c = 0)
Với x = 1 ⇒ y = x2 = 1
Với x = - 2 ⇒ y = x2 = 4
Vậy tọa độ giao điểm của (P) và (d) là (1; 1) và (-2; 4)
c) Do d' // d nên phương trình của d' có dạng: y = -x + b (b ≠ 2)
Gọi A là giao điểm của d' và (P). A có hoành độ -1 ⇒ tung độ của A là 1
Do A (-1; 1) nên tọa độ của A thỏa mãn phương trình đường thẳng d'
⇒ 1 = -(-1) + b ⇒ b = 0
⇒ Phương trình đường thẳng d' là y = -x.
Bài 3: x2 + (m – 2)x – m + 1 = 0
a) phương trình có 1 nghiệm x = 2 nên :
22 + (m-2).2 - m + 1 = 0
⇔ m = -1
Với m = -1, phương trình trở thành: x2 – 3x + 2 = 0
Theo hệ thức Vi-et ta có: x1 + x2 = 3
Giả sử x1 = 2 ⇒ x2 = 1
Vậy với m = - 1 thì phương trình có 1 nghiệm là 2 và nghiệm còn lại là 1.
b) Δ = (m - 2)2 -4.(-m + 1) = m2 - 4m + 4 + 4m - 4 = m2 ≥ 0 ∀ m
⇒ Phương trình đã cho luôn có nghiệm với mọi m
c) Theo hệ thức Vi- et ta có:
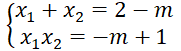
A = x12 + x22 -6x1 x2 = (x1 + x2 )2 - 8x1 x2
= (2 - m)2 - 8(-m + 1) = m2 - 4m + 4 + 8m - 8
= m2 + 4m - 4 = (m + 2)2 - 8
Ta có: (m + 2)2 ≥ 0 ∀ m
⇒ (m + 2)2 - 8 ≥ -8 ∀ m ⇔ A ≥ -8 ∀ m
Dấu bằng xảy ra khi (m + 2)2 = 0 ⇔ m= -2
Vậy GTNN của A là -8, đạt được khi m = -2
Bài 4:
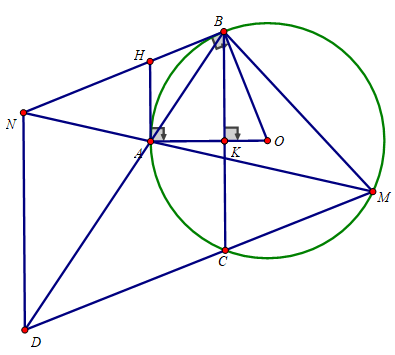
a) Xét tứ giác OBHA có:
∠(OBH) = 90o ( BH là tiếp tuyến của (O)
∠(OAH) = 90o (AH là tiếp tuyến của (O)
⇒ ∠(OBH) + ∠(OAH) = 180o
⇒ Tứ giác OBHA là tứ giác nội tiếp
b) Ta có: Một phần đường kính OA vuông góc dây BC
⇒ AB = AC ⇒ sđ cung AB = sđ cung AC
⇒ ∠(BAH) = ∠(ABC) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn 2 cung bằng nhau)
Tứ giác ABMC nội tiếp (O)
⇒ ∠(NMC) = ∠(ABC) (2 góc nội tiếp cùng chắn cung AC)
Do đó: ∠(NMC) = ∠(BAH)
c) 2 tiếp tuyến HA và HB cắt nhau tại H
⇒ ΔHAB cân tại H ⇒ ∠(BAH) = ∠(HBA)
Theo ý b) ∠(NMC) = ∠(BAH)
⇒ ∠(NMC) = ∠(HBA)
Xét tứ giác MBND có: ∠(NMC) = ∠(HBA)
⇒ 2 đỉnh M và B cùng nhìn cạnh ND dưới 1 góc bằng nhau
⇒ MBND là tứ giác nội tiếp.
d) Xét tứ giác MBND nội tiếp có:
∠(BDN) = ∠(BMN) (2 góc nội tiếp cùng chắn cung BN)
Xét tứ giác ABMC nội tiếp (O) có:
∠(ABC) = ∠(BMN) (2 góc nội tiếp cùng chắn cung bằng nhau )
⇒ ∠(BDN) = ∠(ABC)
Mà 2 góc này ở vị trí so le trong
⇒ ND // BC
Mà BC ⊥ OA ⇒ ND ⊥ OA