Phần trắc nghiệm (3 điểm)
Câu 1 (0,5 điểm)
Trong mặt phẳng Oxy, cho v (-2;1) và điểm M(-3;2). Ảnh của điểm M qua phép tịnh tiến theo vectơ v là điểm có tọa độ nào trong các tọa độ sau đây?
| A.(-1;1) | B.(1;-1) | C.(-5;3) | D.(5;-3) |
Câu 2 (0,5 điểm)
Trong mặt phẳng Oxy, cho 2 điểm A(1/2;2/3) và B(3/2;-1/3). Vectơ v biến đường thẳng (AB) thành chính nó có tọa độ là:
| A.(1;1) | B.(2;1/3) | C.(-2;-1/3) | D.(1;-1) |
Câu 3 (0,5 điểm)
Trong mặt phẳng Oxy, cho đường thẳng (d): 3x-2y+2=0. Ảnh của đường thẳng (d) qua phép đối xứng trục Ox có phương trình là:
A.3x+2y+2=0 B.-3x+2y+2=0
C.3x+2y-2=0 D.3x-2y+2=0
Câu 4 (0,5 điểm)
Tập giá trị của hàm số y = 4cos2x-3sin2x+6 là:
A.[3;10] B.[6;10] C.[-1;13] D.[1;11]
Câu 5 (0,5 điểm)
Hệ số của x3 trong khai triển (x+2/x2)6 bằng:
A.12 B.8 C.6 D.2
Câu 6 (0,5 điểm)
Cho dãy số (un) biết un=3n. Số hạng un-1 bằng:
A.3n-1 B.1/3.3n C.3n-3 D.3n-1
Phần tự luận (7 điểm)
Bài 1 (1 điểm)
Cho ΔABC chứng minh rằng: cosA+cosB+cosC= 1 + 4sinA/2.sinB/2.sinC/2.
Bài 2 (2 điểm)
Giải phương trình: (1-tanx)(1+sin2x)=1+tanx.
Bài 3 (1 điểm)
Cho tập E={1,2,3,4,5,6,7}. Tìm dãy các số tự nhiên gồm 5 chữ số khác nhau lấy từ 7 số trên.
Bài 4 (1 điểm)
Cho dãy số (un) với Đề kiểm tra Toán 11 có đáp án
Tìm xem 7/10 là số hạng thứ mấy của dãy số?
Bài 5 (2 điểm)
Cho 2 đường tròn (C1) và (C2) lần lượt có tâm O1, O2 và đều có bán kình R. Chứng minh rằng (C2) là ảnh của (C1) qua phép đồi xứng trục (d), với (d) là trung trực đoạn O1O2.
ĐÁP ÁN
Phần trắc nghiệm
Câu 1: Đáp án C
Lời giải:
Ta biết rằng phép tịnh tiến theo vectơ v→ (a;b) biến điểm M(x;y) thành điểm M’(x’;y’) với:
Câu 2: Đáp án D
Lời giải:
Để phép tịnh tiến theo vectơ v→ biến (AB) thành chính nó thì vectơ phải có giá song song với (AB).
Ta có: Đề kiểm tra Toán 11 có đáp án
ứng với đáp án D.
Câu 3: Đáp án A
Lời giải:
Mỗi điểm M’(x;y) ∈ (d’) là ảnh của 1 điểm M(xo;yo) ∈ (d) qua phép đối xứng trục Ox, ta có:
Phương trình (*) chính là phương trình của (d’).
Câu 4: Đáp án D
Lời giải:
Ta biến đổi: y=4cos2x-3sin2x+6 4cos2x-3sin2x=y-6(*)
Phương trình (*) có nghiệm khi và chỉ khi:
⇔ -5 ≤ y - 6 ≤ 5 ⇔ 1 ≤ y ≤ 11
Vậy tập giá trị của hàm số là [1;11].
Câu 5: Đáp án A
Lời giải:
Ta có
Do đó hệ số của x3 trong khai triển C6k.2k với k thỏa mãn:
6-3k=3 ⇔ k=1.
Vậy hệ số của x3 trong khai triển bằng C16 = 12
Câu 6: Đáp án B
Phần tự luận
Bài 1:
Lời giải:
Ta có: VT = cosA + cosB + cosC = (cosA + cosB) + cosC
Bài 2:
Lời giải:
Điều kiện
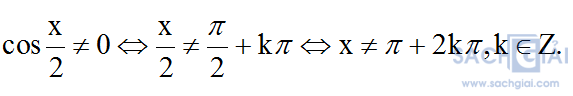
Đặt t=tanx, suy ra
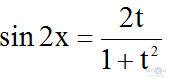
Khi đó, phương trình có dạng:
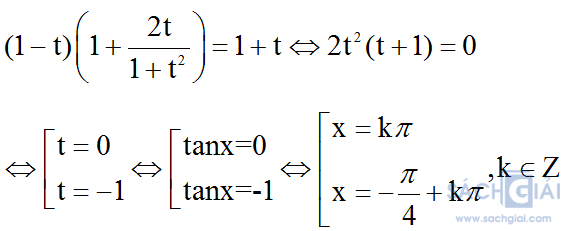
Vậy phương trình có 2 họ nghiệm.
Bài 3:
Lời giải:
Số các số tự nhiên gồm 5 chữ số phân biệt hình thành từ E bằng A75 = 2520.
Bài 4:
Lời giải:
u8= 7/10
Bài 5:
Lời giải:
Lấy M1 tùy ý thuộc (C1) và gọi M2 là ảnh của M qua Sd.
Vì O2M2 và O1M1 đối xứng qua (d) nên ta có O2M2=O1M1.
Ta có: M1 ∈ (C1) ⇔ O1M1=R
⇔O2M2=R⇔M2 (C2)
Ngược lại: lấy M2 là 1 điểm tùy ý thuộc (C2) và gọi M1 là tạo ảnh của nó qua Sd.
Ta có: M2 (C2)⇔ O2M2=R⇔O1M1=R => M1 (C1).
Vậy (C2) là ảnh của (C1) qua Sd.