TRẮC NGHIỆM (3 điểm)
Câu 1 (0,5 điểm)
Trong mặt phẳng Oxy, cho v (2;3) và điểm M(1;-2). Ảnh của điểm M qua phép tịnh tiến theo vectơ v là điểm có tọa độ nào trong các tọa độ sau đây?
A.(3;1) B.(1;5) C.(-1;-5) D.(-3;-1)
Câu 2 (0,5 điểm)
Trong mặt phẳng Oxy, cho đường thẳng (d): 2x+y+1=0. Để phép tịnh tiến theo vectơ v biến (d) thành chính nó thì v phải là vectơ nào trong các trường hợp sau:
A.v→ (2;1) B.v→ (2;-1) C.v→(1;2) D.v → (-1;2)
Câu 3 (0,5 điểm)
Trong mặt phẳng Oxy, cho đường thẳng (d): (x-1)/2=(y-1)/3. Ảnh của đường thẳng (d) qua phép đối xứng trục Ox có phương trình là:
A.3x+2y-1=0 B.3x+2y+1=0
C.3x-2y-1=0 D.3x-2y+1=0
Câu 4 (0,5 điểm)
Khi x thay đổi trong khoảng (5π/4;7π/4) thì y=sinx lấy mọi giá trị thuộc:
A.[√2/2;1] B.[-1;-√2/2] C.[-√2/2;0] D.[-1;1]
Câu 5 (0,5 điểm)
Biết hệ số của x2 trong khai triển (1-3x)n là 90. Giá trị của n là:
A.8 B.5 C.3 D.2
Câu 6 (0,5 điểm)
Cho dãy số (un) biết un=3n. Số hạng u2n-1 bằng:
A.32.3n-1 B.3n.3n-1 C.32n-1 D.32n
TỰ LUẬN (7 điểm)
Bài 1 (1 điểm)
Cho ΔABC chứng minh rằng:
sin2 A+ sin2B+ sin22C = 2+2cosA.cosB.cosC
Bài 2 (2 điểm)
Cho phương trình: cot2x+ m/sinx+ 2m-1=0
a. Giải phương trình với m=1.
b. Tìm m để phương trình có nghiệm thuộc (-π/6;π/6).
Bài 3 (2 điểm)
Với 5 chữ số 1,2,3,4,5 có thể lập được bao nhiêu số gồm 5 chữ số phân biệt và là:
a. Số lẻ
b. Số chẵn
Bài 4 (2 điểm)
Cho 2 hình vuông ABCD và AMNP có cạnh bằng a. Chứng minh rằng tồn tại 1 phép đối xứng trục biến hình vuông ABCD thành AMNP.
ĐÁP ÁN
Câu 1: Đáp án A
Giải:
Ta biết rằng phép tịnh tiến theo vectơ c→ biến điểm M(x;y) thành điểm M’(x’;y’) với:
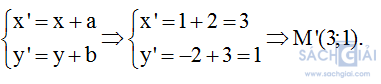
Câu 2: Đáp án D
Giải:
Để phép tịnh tiến theo vectơ v→ biến (d) thành chính nó thì vectơ v→ phải có giá song song với đường thẳng (d).
Nhận xét rằng đường thẳng (d) có vectơ chỉ phương a→ (-1;2).
Do đó, chúng ta chọn đáp án D.
Câu 3: Đáp án A
Giải:
Chuyển phương trình đường thẳng (d) về dạng tổng quát: (d):3x-2y-1=0.
Mỗi điểm M’(x;y) ∈ (d) là ảnh của 1 điểm M(xo; yo) qua phép đối xứng trục Ox, ta có:
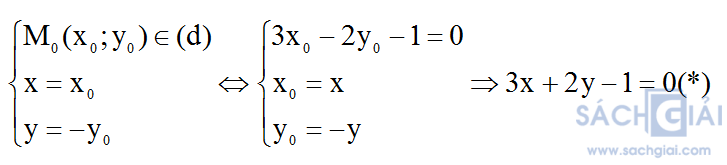
Phương trình (*) chính là phương trình của (d’).
Câu 4: Đáp án B
Giải:
Sử dụng đường tròn đơn vị.
Câu 5: Đáp án B
Giải:
Ta có:
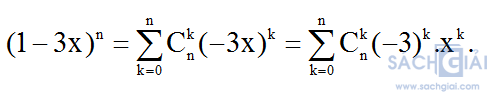
Do đó, hệ số của x2 trong khai triển bằng: Cn2. (-3)2 =90 ⇔ n=5.
Câu 6: Đáp án B
TỰ LUẬN
Bài 1:
Giải:
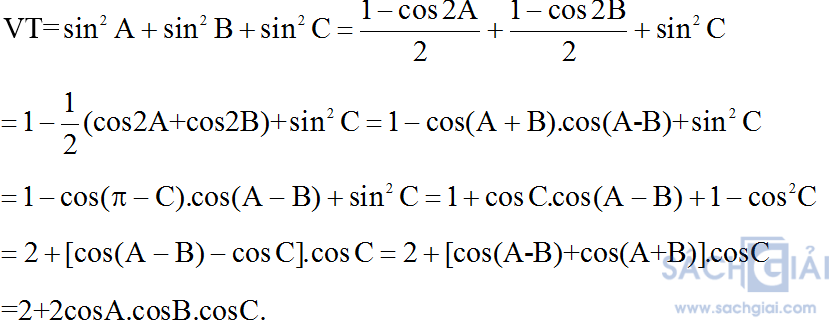
Bài 2:
Giải:
Điều kiện sinx ≠ 0 ⇔ x ≠ kπ, k ∈ Z
Viết lại phương trình dưới dạng:
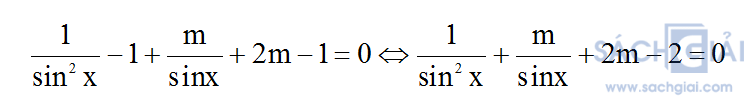
Đặt t= 1/sinx , điều kiện |t| ≥ 1 . Khi đó, phương trình có dạng:
f(t) = t2 + mt + 2m - 2 = 0 (1)
a. Với m=1, ta được:
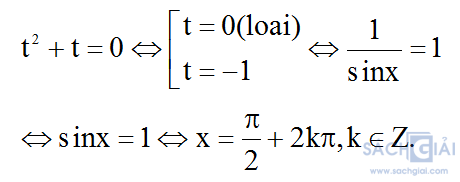
Vậy với m=1 phương trình có 1 họ nghiệm.
b. Phương trình có nghiệm thuộc (-π/6 ; π/6)
=⇔ Phương trình (2) có nghiệm
Ta đi xét bài toán ngược “Tìm điều kiện của m để phương trình (1) vô nghiệm hoặc cả 2 nghiệm đều thuộc khoảng (-2;2)”.
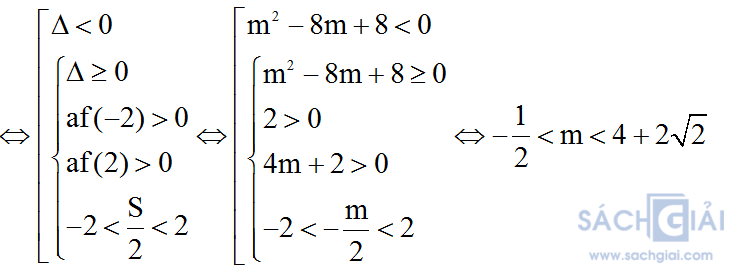
Vậy với m ≤ -1/2 hoặc m ≥ 4 + 2√2 thỏa mãn điều kiện đầu bài.
Bài 3:
Giải:
Sử dụng kiến thức hoán vị:
a5 được chọn từ tập F={1,3,5} => có 3 cách chọn.
a1,a2,a3,a4 là 1 bộ phân biệt thứ tự được chọn từ E\{a5} do đó nó là 1 hoán vị của 4 phần tử => có P4 cách chọn.
Theo quy tắc nhân, số các số lẻ gồm 5 chữ số phân biệt, hình thành từ tập E, bằng: 3.P4=3.4!=72 số.
b. Tương tự câu a) ta được kết quả = 48 số.
Bài 4:
Giải:
Giả sử CD cắt MN tại E, ta đi chứng minh: S(AE)(ABCD)= APNM
Thật vậy:
ΔAED = ΔAEM => M = S(AE)(D)
ΔAEC = ΔAEN => N = S(AE)(C)
ΔAEB = ΔAEP => P = S(AE)(B)