Giải Sách bài tập Toán 6 bài 13: Ước và bội

Thứ hai - 07/10/2019 10:53

Hướng dẫn giải chi tiết: Sách bài tập Toán 6 - Bài 13: Ước và bội

141. a. Viết tập hợp các bội nhỏ hơn 40 của 7.
b. Viết dạng tổng quát các số là bội của 7.
Giải:
a. Ta có: B(7) = {0; 7; 14; 21; 28; 35; 42;...}
Vậy tập hợp các bội nhỏ hơn 40 của 7 là {0; 7; 14; 21; 28; 35}
b. Dạng tổng quát các số là bội của 7 là 7k với k ∈ N.

142. Tìm các số tự nhiên x sao cho:
a. x ∈ B(15) và 40 ≤ x ≤ 70
b. x ⁞ 12 và 0 < x ≤ 30
c. x ∈ Ư(30) và x > 12
d. 8 : x
Giải:
a. Ta có: B(15) = {0; 15; 30; 45; 60; 75;...}
Vì x ∈ B(15) và 40 ≤ x ≤ 70 nên x ∈ {45; 60}
b. Vì x ⁞ 12 nên x là bội của 12
Ta có: B(12) = {0; 12; 24; 36; 48;...}
Vì x ⁞ 12 và 0 < x ≤ 30 nên x ∈ {12; 24}
c. Ta có: Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
Vì x ∈ Ư(30) và x > 12 nên x ∈ {15; 30}
d. Vì 8 ⁞ x nên x là ước của 8
Ta có: Ư(8) = {1; 2; 4; 8}
Vậy x ∈ {1; 2; 4; 8}

143. Tuấn có 42 chiếc tem. Tuấn muốn chia đều số tem đó vào các phong bì. Trong các cách chia sau, cách nào thực hiện được? Hãy điền vào chỗ trống trong trường hợp chia được.

Cách chia	Số phong bì	Số tem trong một phong bì
Thứ nhất Thứ hai Thứ ba	3 ..... 8	....... 7 .......

Giải:
Vì 42 ⁞ 3 nên cách thứ nhất thực hiện được. Số tem trong một phong bì là 42 ⁞ 3 = 14 (tem)
Vì 42 ⁞ 7 nên cách thứ hai thực hiện được. Số phong bì chứa tem là 42 : 7 = 6 (bì)
Vì 42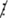

8 nên cách thứ ba không thực hiện được.

Cách chia	Số phong bì	Số tem trong một phong bì
Thứ nhất	3	14
Thứ hai	6	7
Thứ ba	8	...

144. Tìm tất cả các số có hai chữ số là bội của:
a. 32
b. 41
Giải:
a. Ta có: B(32) = {0; 32; 64; 96; 128;...}
Các số có hai chữ số là bội của 32 là {32; 64; 96}
b. Ta có: B(41) = {0; 41; 82; 123; ...}
Các số có hai chữ số là bội của 41 là {41; 82}

145. Tìm tất cả các số có hai chữ số là ước của:
a. 50
b. 45
Giải:
a. Ta có: Ư(50) = {1; 2; 5; 10; 25; 50}
Các số có hai chữ số là ước của 50 là {10; 25; 50}
b. Ta có: Ư(45) = {1; 3; 5; 9; 15; 45}
Các số có hai chữ số là ước của 45 là {15; 45}

146. Tìm các số tự nhiên x sao cho:
a. 6 ⁞ (x - 1)
b. 14 ⁞ (2x + 3)
Giải:
a. Vì 6 ⁞ (x - 1) nên (x - 1) ∈ Ư(6)
Ta có: Ư(6) = {1; 2; 3; 6}
Suy ra: x - 1 = 1 <=> x = 2
x - 1 = 2 <=> x = 3
x - 1 = 3 <=> x = 4
x - 1 = 6 <=> x = 7
Vậy x ∈ {2; 3; 4; 7} thì 6 ⁞ (x - 1).
b. Vì 14 ⁞ (2x + 3) nên (2x + 3) ∈ Ư(14)
Ta có: Ư(14) = {1; 2; 7; 14}
Vì 2x + 3 ≥ 3 nên (2x + 3) ∈ {7; 14}
Suy ra: 2x + 3 = 7 <=> 2x = 4 <=> x = 2
2x + 3 = 14 <=> 2x = 11 => x ∉ N (loại)
Vậy x = 2 thì 14 ⁞ (2x + 3).

147. Có bao nhiêu bội của 4 từ 12 đến 200?
Giải:
Vì trong bốn số tự nhiên thì có một số là bội của 4 nên số bội của 4 từ 12 đến 200 là:
(200 - 12) : 4 + 1 = 188 : 4 + 1 = 47 + 1 = 48 (số)

Bản quyền bài viết thuộc về Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.

Ý kiến bạn đọc