Giải Sách bài tập Toán 6 bài 11: Dấu hiệu chia hết cho 2, cho 5

Thứ hai - 07/10/2019 10:33

Hướng dẫn giải chi tiết: Sách bài tập Toán 6 - Bài 11: Dấu hiệu chia hết cho 2, cho 5

123. Trong các số: 213; 435; 680; 156:
a. Số nào chia hết cho 2 mà không chia hết cho 5?
b. Số nào chia hết cho 5 mà không chia hết cho 2?
c. Số nào chia hết cho cả 2 và 5?
d. Số nào không chia hết cho cả 2 và 5?
Giải:
a. Số chia hết cho 2 mà không chia hết cho 5 là số có chữ số tận cùng là số chẵn nhưng khác số0. Ta có số 156.
b. Số chia hết cho 5 mà không chia hết cho 2 là số có chữ số tận cùng là 5. Ta có số 435.
c. Số chia hết cho cả 2 và 5 là số có chữ số tận cùng là 0. Ta có số 680.
d. Số không chia hết cho cả 2 và 5 là số có chữ số tận cùng là số lẻ nhưng khác số 5. Ta có số 213.

124. Tổng (hiệu) sau có chia hết cho 2 không, có chia hết cho 5 không?
a. 1 .2.3.4.5 + 52
b. 1.2.3.4.5 - 75
Giải:
a. Ta có: 1.2.3.4.5 ⁞ 2; 52 ⁞ 2 suy ra: (1.2.3.4.5 + 52) ⁞ 2
1.2.3.4.5 ⁞ 5; 52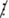

5 suy ra: (1.2.3.4.5 + 52)

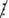5
b. Ta có:1.2.3.4.5 ⁞ 2; 75

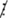2 suy ra: (1.2.3.4.5 - 75)

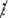2
1.2.3.4.5 ⁞ 5; 75 ⁞ 5 suy ra: (1.2.3.4.5 - 75) ⁞ 5
125. Điền chữ số vào dấu * để được số 35*:
a. Chia hết cho 2
b. Chia hết cho 5
c. Chia hết cho cả 2 và 5
Giải:
a. Số 35* chia hết cho 2 nên chữ số tận cùng phải là chữ số chẵn.
Vậy dấu * được thay bởi các chữ số 0; 2; 4; 6; 8 thì được số chia hết cho 2.
b. Số 35* chia hết cho 5 nên chữ số tận cùng phải là chữ số 0 hoặc chữ số 5.
Vậy dấu * được thay bởi các chữ số 0; 5 thì được số chia hết cho 5.
c. Số 35* chia hết cho 2 và 5 nên chữ số tận cùng phải là chữ số 0. Vậy dấu * được thay bởi chữ số 0 thì được số chia hết cho 2 và 5.

126. Điền chữ số vào dấu * để được số *45:
a. Chia hết cho 2
b. Chia hết cho 5
Giải:
a. Vì số *45 có chữ số tận cùng là số lẻ nên không chia hết cho 2. Như vậy không có chữ số nào thay vào dấu * để được số chia hết cho 2.
b. Vì số *45 có chữ số tận cùng là số 5 nên chia hết cho 5. Như vậy thay vào dấu * bằng các chữ số từ 0 đến 9 thì được số chia hết cho 5.

127. Dùng ba chữ số 6, 0, 5, hãy ghép thành các số tự nhiên có ba chữ số thỏa mãn một trong các điều kiện:
a. Số đó chia hết cho 2
b. Số đó chia hết cho 5
Giải:
a. Đế được số chia hết cho 2 thì chữ số tận cùng cúa số đó phải là số chẵn. Như vậy, ta có các số: 560, 506, 650.
b. Để được số chia hết cho 5 thì chữ số tận cùng của số đó phải là 0 hoặc 5. Như vậy, ta có các số: 560, 650, 605.

128. Tìm số tự nhiên có hai chữ số, các chữ số giống nhau, biết rằng số đó chia hết cho 2, còn chia cho 5 thì dư 4.
Giải:
Vì số cần tìm chia hết cho 2 nên số tận cùng phải là số chẵn.
Như vậy, số tự nhiên có hai chữ số, các chữ số giống nhau và chia hết cho 2 là 22, 44, 66, 88.
Ta có: 22 chia cho 5 dư 2
44 chia cho 5 dư 4
66 chia cho 5 dư 1
88 chia cho 5 dư 3
Vậy số cần tìm là 44.

129. Dùng cả ba chữ số 3, 4, 5, hãy ghép thành các số tự nhiên có ba chữ số:
a. Lớn nhất và chia hết cho 2
b. Nhỏ nhất và chia hết cho 5
Giải:
a. Vì số cần tìm chia hết cho 2 nên chữ số tận cùng phải là 4; số lớn nhất nên chữ số hàng trăm là 5. Vậy số cần tìm là 534.
b. Vì số cần tìm chia hết cho 5 nên chữ số tận cùng phải là 5; số nhỏ nhất nên chữ số hàng trăm là 3. Vậy số cần tìm là 345.

130. Tìm tập hợp các số tự nhiên n vừa chia hết cho 2, vừa chia hết cho 5 và 136 < n < 182.
Giải:
Vì các số tự nhiên chia hết cho 2 và 5 nên chữ số tận cùng là 0.
Mà 136 < n < 182 nên ta có: n = {140; 150; 160; 170; 180}.

131. Từ 1 đến 100 có bao nhiêu số chia hết cho 2, có bao nhiêu số chia hết cho 5?
Giải:
Vì cứ hai số tự nhiên thì có một số chia hết cho 2 nên trong khoảng từ 1 đến 100 có các số chia hết cho 2:
(100 - 2) : 2 + 1 = 50 (số)
Vì cứ năm số tự nhiên thì có một số chia hết cho 5 nên trong khoảng từ 1 đến 100 có các số chia hết cho 5:
(100 - 5) : 5 + 1 = 20 (số)

132. Chứng tỏ rằng với mọi số tự nhiên n thì tích (n + 3)(n + 6) chia hết cho 2.
Giải:
* Nếu n : 2 thì n = 2k (k ∈ N)
Suy ra: n + 6 = 2k + 6
Vì (2k + 6) ⁞ 2 nên (n + 3)(n + 6) ⁞ 2
* Nếu n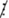

2 thì n = 2k + 1 (k ∈ N)
Suy ra: n + 3 = 2k + 1 + 3 = 2k + 4
Vì (2k + 4) ⁞ 2 nên (n + 3)(n + 6) ⁞ 2
Vậy (n + 3)(n + 6) chia hết cho 2 với mọi số tự nhiên n.

Bản quyền bài viết thuộc về Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.

Ý kiến bạn đọc