Giải Sách bài tập Toán 6 bài 4: Số phần tử của tập hợp. Tập hợp con

Chủ nhật - 06/10/2019 11:37

Hướng dẫn giải chi tiết: Sách bài tập Toán 6 bài 4: Số phần tử của tập hợp. Tập hợp con

29. Viết các tập hợp sau và cho biết mỗi tập hợp có bao nhiêu phần tử?
a. Tập hợp A các số tự nhiên x mà x - 5 = 13
b. Tập hợp B các số tự nhiên x mà x + 8 = 8
c. Tập hợp c các số tự nhiên x mà x.0 = 0
d. Tập hợp D các số tự nhiên x mà x.0 = 7
Giải:
a. Ta có: x - 5 = 13 => x = 18. Vậy A = {18}. Tập hợp A có một phần tử.
b. Ta có: x + 8 = 8 => x = 0. Vậy B = {0}. Tập hợp B có một phần tử.
c. Ta có: x.0 = 0 => x ∊ N . Vậy C = N
Tập hợp C có vô số phần tử.
d. Không có giá trị nào của c thỏa x.0 = 7. Vậy D = Ø
Tập hợp D không có phần tử nào.

30. Viết các tập hợp sau và cho biết mỗi tập hợp có bao nhiêu phần tử?
a. Tập hợp các số tự nhiên không vượt quá 50.
b. Tập hợp các số tự nhiên lớn hơn 8 nhưng nhỏ hơn 9.
Giải:
a. Tập hợp các số tự nhiên không vượt quá 50: A = {1; 2; 3; ...; 50}
Tập hợp A có (50 - 0) + 1 = 51 phần tử.
b. Vì 8 và 9 là hai số tự nhiên liên tiếp nên không có số tự nhiên nào lớn hơn 8 nhưng nhỏ hơn 9. Vậy B = Ø.
Tập hợp B không có phần tử nào.

31. Cho A = {0}. Có thể nói rằng A = 0 hay không?
Giải:
Không thể nói A = 0 vì tập hợp rỗng không có phần tử nào trong khi đó tập hợp A có một phần tử là 0.

32. Viết tập hợp A các số tự nhiên nhỏ hơn 6, tập hợp B các số tự nhiên nhỏ hơn 8, rồi dùng kí hiệu ⊂ để thể hiện mối quan hệ giữa hai tập hợp trên.
Giải
Tập hợp A = {0; 1; 2; 3; 4; 5}
Tập hợp B = {0; 1; 2; 3; 4; 5; 6; 7}
Ta có: A ⊂ B

33. Cho tập hợp A = {8; 10}. Điền kí hiệu ∈, ⊂ hoặc = vào ô vuông:
giai sbt toan 6 bai 4 cau 33

34. Tính số phần tử của các tập hợp:
a. A = {40; 41; 42; ...; 99; 100}
b. B = {10; 12; 14; ...; 96; 98}
c. C = {35; 37; 39; ...; 103; 105}
Giải:
a. Tập hợp A gồm các số tự nhiên liên tiếp từ 40 đến 100 nên số phần tử của A là: (100 - 40) + 1 = 61
Vậy tập hợp A có 61 phần tử.
b. Tập hợp B gồm các số tự nhiên chẵn liên tiếp từ 10 đến 98 nên số phần tử của B là: (98 - 10) : 2 + 1 = 88 : 2 + 1 = 45
Vậy tập hợp B có 45 phần tử.
c. Tập hợp C gồm các sô tự nhiên lẻ liên tiếp từ 35 đến 105 nên số phần tử của C là: (105 - 35) : 2 + l = 70 : 2 + l = 36
Vậy tập hợp C có 36 phần tử.

35. Cho hai tập hợp: A = {a, b, c, d}, B = {a, b}
a. Dùng kí hiệu ⊂ để thể hiện quan hệ giữa hai tập hợp A và B.
b. Dùng hình vẽ minh họa hai tập hợp A và B.
Giải
a. Ta có: B ⊂ A.
b.
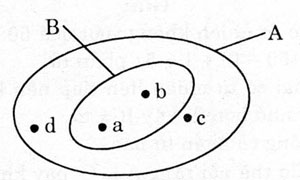
giai sbt toan 6 bai 4 cau 35

36. Cho tập hợp A = {1; 2; 3}. Trong các cách viết sau, cách viết nào đúng, cách viết nào sai?
1 ∈ A          {1} ∈ A      3 ⊂ A         {2; 3} ⊂ A
Giải
1 ∈ A đúng                    {1} ∈ A sai
3 ⊂ A sai {2; 3} ⊂ A đúng.

37. Cho ví dụ hai tập hợp A và B mà A ⊂ B và B ⊂ A.
Giải
Ví dụ: A = {cam, quýt, bưởi}
           B = {quýt, bưởi, cam}

38. Cho tập hợp M = {a, b, c}. Viết các tập hợp con của tập hợp M sao cho mỗi tập hợp con đó có hai phần tử.
Giải:
Các tập hợp con của tập hợp M = {a, b, c} mà mỗi tập hựp con đó có hai phần tử: {a, b}, {a, c}, {b, c}

39. Gọi A là tập hợp các học sinh của lớp 6A có hai điểm 10 trở lên, B là tập hợp các học sinh của lớp 6A có 3 điểm 10 trở lên, M là tập hợp các học sinh của lớp 6A có 4 điểm 10 trở lên. Dùng kí hiệu ⊂ để thể hiện quan hệ giữa hai trong ba tập hợp trên.
Giải
B ⊂ A, M ⊂ B, M ⊂ A

40. Có bao nhiêu số tự nhiên có bốn chữ số?
Giải
Số tự nhiên có bốn chữ số bao gồm: {1000; 1001; 1002; ..., 9999}
Vậy có: (9999 - 1000) + 1 = 9000 số.

41. Có bao nhiêu số chẵn có ba chữ số?
Giải
Sô tự nhiên chẵn có ba chữ số gồm: {100; 102; 104; ...; 998}
Vậy có: (998 - 100) : 2 + 1 = 449 + 1 = 450 số.

42. Bạn Tâm đánh số trang bằng các số tự nhiên từ 1 đến 100. Bạn Tâm phải viết tất cả bao nhiêu chữ số?
Giải
Từ 1 đến 9 có 9 số có một chữ số. Bạn Tâm phải viết 9 chữ số.
Từ 10 đến 99 có (99 - 10) + 1 = 90 số có hai chữ số. Bạn Tâm phải viết 2.90 = 180 chữ số.
Số 100 có 3 chữ số. Bạn Tâm phải viết 3 chữ số.
Vậy bạn Tâm phải viết tất cả: 9 + 180 + 3 = 192 chữ số.

Bản quyền bài viết thuộc về Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.

Ý kiến bạn đọc