Giải Sách bài tập Toán 6 chương 1 bài 18: Sách bài tập Toán 6 chương 1 bài 18: Bội chung nhỏ nhất

188. Tìm BCNN của:
a. 40 và 52
b. 42, 70 và 180
c. 9, 10 và 11
Giải:
a. 40 = 2³.5                    52 = 2².13
BCNN (40; 52) = 2³.5.13 = 520
b. 42 = 2.3.7                  70 = 2.5.7             180 = 2².3².5
BCNN (42; 70; 180) = 2².3².5.7 = 1260
c. Vì 9, 10 và 11 là các số đôi một nguyên tố cùng nhau nên:
BCNN (9; 10; 11) = 9.10.11 = 990

189. Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a ⁞ 126 và a ⁞ 198.
Giải:
Vì a ⁞ 126 và a ⁞ 198 nên a ∈ BC (126; 198)
Vì a là số tự nhiên nhỏ nhất nên a ∈ BCNN (126; 198)
Ta có: 126 = 2.3².7                  198 = 2.3².11
BCNN (126; 198) = 2.3².7.11 = 1386.
Vậy a = 1386.

190. Tìm các bội chung của 15 và 25 mà nhỏ hơn 400.
Giải:
Ta có: 15 = 3.5              25 = 5²
BCNN (15; 25) = 3.5² = 75
BC (15; 25) = {0; 75; 150; 225; 300; 375; 450;...}
Bội chung của 15 và 25 mà nhỏ hơn 400 là:
{0; 75; 150; 225; 300; 375}

191. Một số sách khi xếp thành từng bó 10 cuốn, 12 cuốn, 15 cuốn, 18 cuốn đều vừa đủ bó. Biết số sách trong khoảng từ 200 đến 500. Tính số sách đó.
Giải:
Gọi m (m ∈ N*) là số sách cần tìm.
Vì xếp thành từng bó 10 cuốn, 12 cuốn, 15 cuốn, 18 cuốn đều vừa đủ bó nên số sách m ∈ BC (10; 12; 15; 18).
Ta có: 10 = 2.5              12 = 2².3
           15 = 3.5              18 = 2.3²
BCNN (10; 12; 15; 18) = 2².3².5 = 180
BC (10; 12; 15; 18) = {0; 180; 360; 540; ...}
Vì số sách trong khoảng từ 200 đến 500 nên m = 360.
Vậy có 360 cuốn sách.

192. Hai bạn Tùng và Hải thường đến thư viện đọc sách. Tùng cứ 8 ngày đến thư viện một lần, Hải 10 ngày một lần. Lần đầu cả hai bạn cùng đến thư viện vào một ngày. Hỏi sau ít nhất bao nhiêu ngày thì hai bạn cùng đến thư viện?
Giải:
Gọi m (m ∈ N*) là ngày cần tìm.
Vì số ngày ít nhất nên m là BCNN của 8 và 10.
Ta có: 8 = 2³                  10 = 2.5
BCNN (8; 10) = 2³.5 = 40
Vậy sau 40 ngày thì hai bạn cùng đến thư viện vào một ngày.

193. Tìm các bội chung có ba chữ số của 63, 35 và 105.
Giải:
Ta có: 63 = 3².7             35 = 5.7                105 = 3.5.7
BCNN (63; 35; 105) = 3².5.7 = 315
BC (63; 35; 105) = {0; 315; 630; 945; 1260; ...}
Bội chung có ba chữ số của 63, 35 và 105 là:
{315; 630; 945}

194. Cho biết m ⁞ n, tìm BCNN (m; n). Cho ví dụ.
Giải:
Vì m ⁞ n nên BCNN (m; n) = m
Ví dụ: 12 ⁞ 4 nên BCNN (12; 4) = 12

195. Một liên đội thiếu niên khi xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người. Tính số đội viên của liên đội biết rằng số đó trong khoảng từ 100 đến 150.
Giải:
Gọi m (m ∈ N * và 100 ≤ m ≤ 150) là số đội viên của liên đội.
Vì xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người nên:
(m-1)⁞ 2; (m-1)⁞ 3; (m-1)⁞ 4; (m-1)⁞ 5
Suy ra: (m-1) ∈ BC(2; 3; 4; 5)
Ta có: 2 = 2                   3 = 3
4 = 2²          5 = 5
BCNN (2; 3; 4; 5) = 2².3.5 = 60
BC (2; 3; 4; 5) = {0; 60; 120; 180; ...}
Vì 100 ≤ m ≤ 150 nên m = 120 + 1 = 121
Vậy liên đội có 121 đội viên.

196. Một khối học sinh khi xếp hàng 2, hàng 3, hàng 4, hàng 5, hàng 6 đều thiếu 1 người, nhưng xếp hàng 7 thì vừa đủ. Biết số học sinh chưa đến 300. Tính số học sinh.
Giải:
Gọi m (m ∈ N * và m < 300) là số học sinh của một khối.
Vì xếp hàng 2, hàng 3, hàng 4, hàng 5, hàng 6 đều thiếu 1 người nên:
(m + 1)⁞ 2; (m + 1)⁞ 3; (m + 1)⁞ 4; (m + 1) ⁞ 5; (m + 1) ⁞ 6
Suy ra: (m + 1) ∈ BC(2; 3; 4; 5; 6) và m + 1 < 301
Ta có: 2 = 2
3 = 3
4 = 22
5 = 5
6 = 2.3
BCNN (2; 3; 4; 5; 6) = 2².3.5 = 60
BC (2; 3; 4; 5; 6) = {0; 60; 120; 180; 240; 300; 360...}
Vì m + 1 < 301 nên m + 1 ∈ {60; 120; 180; 240; 300}
Suy ra: m ∈ {59; 119; 179; 239; 299}
Ta có: 59 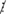 7; 119 ⁞ 7; 179  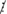7; 239  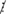7; 299  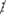7
Vậy khối có 119 học sinh.

197. Một bộ phận của máy có hai bánh xe răng cưa khớp với nhau, bánh xe I có 18 răng cưa, bánh xe II có 12 răng cưa. Người ta đánh dấu “x” vào hai răng cưa khớp với nhau. Hỏi mỗi bánh xe phải quay ít nhất bao nhiêu răng cưa để hai răng cưa đánh dấu ấy khớp lại với nhau ở vị trí giống lần trước? Khi đó mỗi bánh xe đã quay bao nhiêu vòng?
Giải:
Gọi m (m ∈ N*) là số răng cưa phải tìm.
Ta có: m 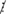12 và m  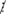18
Vì m nhỏ nhất nên m là BCNN (12; 18)
Ta có: 12 = 2².3
18 = 2.3²
BCNN (12; 18) = 2².3² = 36
Vậy mỗi bánh xe phải quay ít nhất 36 răng cưa để hai răng cưa được đánh dấu “x” khớp với nhau lần nữa. Khi đó:
Bánh xe thứ nhất quay được: 36 : 18 = 2 (vòng)
Bánh xe thứ hai quay được: 36 : 12 = 3 (vòng)