Giải Sách bài tập Toán 6: Ôn tập chương 1 (Phần 1)
2019-10-08T03:50:40-04:00
2019-10-08T03:50:40-04:00
https://sachgiai.com/Toan-hoc/giai-sach-bai-tap-toan-6-on-tap-chuong-1-phan-1-12356.html
/themes/whitebook/images/no_image.gif
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Thứ ba - 08/10/2019 03:48
Hướng dẫn giải chi tiết: Sách bài tập Toán 6: Ôn tập chương 1 (Phần 1)
198. Tìm số tự nhiên x, biết:
a. 123 - 5(x + 4) = 38
b. (3x - 24).73 = 2.74
Giải:
a. 123 - 5.(x + 4) = 38 <=> 5(x + 4) = 123 - 38
<=> 5(x + 4) = 85 <=> x + 4 = 85 : 5 <=> x + 4 = 17
<=> x = 17 - 4 <=> x = 13
b. (3.x – 24).73 = 2.74 <=> 3x - 24 = 2.74 : 73
<=> 3x - 16 = 2.7 <=> 3x - 16 = 14 <=> 3x = 14 + 16
<=> 3x = 30 <=> x = 30 : 3 <=> x = 10
199. Tìm số tự nhiên x, biết rằng nếu chia nó cho 3 rồi trừ 4, sau đó nhân với 5 thì được 15.
Giải:
Theo đề bài, ta có: (x : 3 - 4).5 = 15 <=> x : 3 - 4 = 15 : 5
<=> x : 3 - 4 = 3 <=> x : 3 = 3 + 4
<=> x : 3 = 7 <=> x = 7.3 <=> x = 21
200. Thực hiện phép tính rồi phân tích kết quả ra thừa số nguyên tố:
a. 62 : 4.3 + 2.52
b. 5.42 - 18 : 32
Giải:
a. 62 : 4.3 + 2.52 = 36 : 12 + 2.25 = 3 + 50 = 53
53 là số nguyên tố
b. 5.42 - 18 : 32 = 5.16 - 18 : 9 = 80 - 2 = 78
78 = 2.3.13
201. Tìm số tự nhiên x, biết:
a. 70 ⋮ x, 84 ⋮ x và x > 8
b. x ⋮ 12, x ⋮ 25, x ⋮ 30 và 0 < x < 500
Giải:
a. 70 ⋮ x, 84 ⋮ x và x > 8
Vì 70 ⋮ x và 84 ⋮ x nên x ∈ ƯC (70; 84)
Ta có: 70 = 2.5.7 84 = 22.3.7
ƯCLN (70; 84) = 2.7 = 14
ƯC (70; 84) = {1; 2; 7; 14}
Vì x > 8 nên x = 14.
b. x ⋮ 12, x ⋮ 25, x ⋮ 30 và 0 < x < 500
Vì x ⋮ 12, x ⋮ 25 và x ⋮ 30 nên x ∈ BC (12; 25; 30)
Ta có: 12 = 22.3 25 = 52 30 = 2.3.5
BCNN (12; 25; 30) = 22.3.55 = 300
BC (12; 25; 30) = {0; 300; 600; ...}
Vì 0 < x < 500 nên x = 300.
202. Tìm số tự nhiên nhỏ hơn 200, biết rằng số đó chia cho 2 dư 1, chia cho 3 dư 1, chia cho 5 thiếu 1 (một số chia cho 5 thiếu 1 tức là số đó cộng thêm 1 thì chia hết cho 5) và chia hết cho 7.
Giải:
Gọi m là số tự nhiên cần tìm.
Ta có: m chia cho 2 dư 1 nên m có chữ số tận cùng là số lẻ
m chia cho 5 thiếu 1 nên m có chữ số tận cùng bằng 4 hoặc bằng 9. Vậy m có chữ số tận cùng bằng 9.
m chia hết cho 7 nên m là bội số của 7 mà có chữ số tận cùng bằng 9.
Ta có: 7.7 = 49
7.17 = 119
7.27 = 189
7.37 = 259 (loại vì a < 200)
Trong các số 49, 119, 189 thì chỉ 49 là chia cho 3 dư 1.
Vậy số cần tìm là 49.
203. Thực hiện phép tính:
a. 80 - (4.52 - 3.23)
b. 23.75 + 25.23 + 180
c. 2448: [119-(23-6)]
Giải:
a. 80 - (4.52 - 3.23) = 80 - (4.25 - 3.8)
= 80 - (100 - 24) = 80 - 76 = 4
b. 23.75 + 25.23 + 180 = 23.(75 + 25) + 180
= 23.100 + 180 = 2300 + 180 = 2480
c. 2448 : [119 - (23 - 6)] = 2448 : (119 - 17) = 2448 : 102 = 24
204. Tìm số tự nhiên x, biết:
a. (2600 + 6400) - 3x = 1200
b. [(6x - 72) : 2 - 84].28 = 5628
Giải:
a. (2600 + 6400) - 3x = 1200 <=> 9000 - 3x = 1200
<=> 3x = 9000 - 1200 <=> 3x = 7800 <=> x = 7800 : 3 <=> x = 2600
b. [(6x - 72) : 2 - 84].28 = 5628
<=> (6x - 72) : 2 - 84 = 5628 : 28 <=> (6x - 72) : 2 - 84 = 201
<=> (6x - 72) : 2 = 201 + 84 <=> (6x - 72) : 2 = 285
<=> 6x - 72 = 285.2 <=> 6x - 72 = 570 <=> 6x = 570 + 72
<=> 6x = 642 <=> x = 642 : 6 <=> x = 107
205. Cho A = {8; 45}, B = {15; 4}
a. Tìm tập hợp C các số tự nhiên x = a + b sao cho a ∈ A, b ∈ B
b. Tìm tập hợp D các số tự nhiên x = a - b sao cho a ∈ A, b ∈ B
c. Tìm tập hợp E các số tự nhiên x = a.b sao cho a ∈ A, b ∈ B
d. Tìm tập hợp G các số tự nhiên x sao cho a = b.x và a ∈ A, b ∈ B
Giải:
a. c = {23; 12; 60; 49}
b. D = {4; 30; 41}
c. E = {120; 32; 675; 180}
d. G = {2; 3}
206. Phép nhân kì lạ: Nếu ta nhân số 12 345 679 (không có chữ số 8) với một số a bất kì có một chữ số, rồi nhân kết quả với 9 thì được số có chín chữ số như nhau và mỗi chữ số đều là a.
Ví dụ: 12 345 679 . 7 = 86 419 753
86 419 753 . 9 = 777 777 777
Hãy Giải: thích vì sao?
Giải:
Ta có: 12 345 679.a.9 = (12 345 679.9).a = 111 111 111.a
= 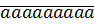 207. Cho tổng A = 270 + 3105 + 150. Không thực hiện phép tính, xét xem tổng A có chia hết cho 2, cho 5, cho 3, cho 9 hay không? Tại sao?
Giải:
270 ⋮ 2; 3105
207. Cho tổng A = 270 + 3105 + 150. Không thực hiện phép tính, xét xem tổng A có chia hết cho 2, cho 5, cho 3, cho 9 hay không? Tại sao?
Giải:
270 ⋮ 2; 3105 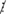 2; 150 ⋮ 2 Suy ra: A
2; 150 ⋮ 2 Suy ra: A 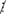 2
270 ⋮ 5; 3105 ⋮ 5; 150 ⋮ 5 Suy ra: A ⋮ 5
270 ⋮ 3; 3105 ⋮ 3; 150 ⋮ 3 Suy ra: A ⋮ 3
270 ⋮ 9; 3105 ⋮ 9; 150
2
270 ⋮ 5; 3105 ⋮ 5; 150 ⋮ 5 Suy ra: A ⋮ 5
270 ⋮ 3; 3105 ⋮ 3; 150 ⋮ 3 Suy ra: A ⋮ 3
270 ⋮ 9; 3105 ⋮ 9; 150 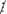 9 Suy ra: A
9 Suy ra: A 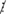 9
208. Tổng sau là số nguyên tố hay hợp số?
a. 2.3.5 + 9.31
b. 5.6.7 + 9.10.11
Giải:
a. Ta có: 2.3.5 + 9.31 > 3
2.3.5 ⋮ 3 và 9.31 ⋮ 3
Vậy tổng 2.3.5 + 9.31 là hợp số.
b. Ta có: 5.6.7 + 9.10.11 > 3
5.6.7 ⋮ 3 và 9.10.11 ⋮ 3
Vậy tổng 5.6.7 + 9.10.11 là hợp số.
209. Điền chữ số vào dấu * để số 1*5* chia hết cho tất cả các số 2, 3, 5, 6, 9.
Giải:
Vì
9
208. Tổng sau là số nguyên tố hay hợp số?
a. 2.3.5 + 9.31
b. 5.6.7 + 9.10.11
Giải:
a. Ta có: 2.3.5 + 9.31 > 3
2.3.5 ⋮ 3 và 9.31 ⋮ 3
Vậy tổng 2.3.5 + 9.31 là hợp số.
b. Ta có: 5.6.7 + 9.10.11 > 3
5.6.7 ⋮ 3 và 9.10.11 ⋮ 3
Vậy tổng 5.6.7 + 9.10.11 là hợp số.
209. Điền chữ số vào dấu * để số 1*5* chia hết cho tất cả các số 2, 3, 5, 6, 9.
Giải:
Vì 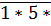 chia hết cho 2 và cho 5 nên chữ số hàng đơn vị là 0.
Vì
chia hết cho 2 và cho 5 nên chữ số hàng đơn vị là 0.
Vì 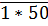 chia hết cho 9 nên 1 + (*) + 5 + 0 = [6 + (*)] ⋮ 9
Suy ra (*) = 3
Vậy ta có số 1350
Vì 1250 ⋮ 9 nên 1350 ⋮ 3
Vì ƯCLN (2; 3) = 1 nên 1350 ⋮ (2; 3) = 6
Vậy số 1350 chia hết cho tất cả các số 2, 3, 5, 6, 9.
210. Tổng sau có chia hết cho 3 không?
A = 2 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 210
Giải:
Ta có: A = 2 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 210
= (2 + 22) + (23 + 24) + (25 + 26) + (27 + 28) + (29 + 210)
= 2.(1 + 2) + 23.(1 + 2) + 25.(1 + 2) + 27.(1 + 2) + 29.(1 + 2)
= 2.3 + 23 3 + 25.3 + 27.3 + 29.3
= 3.(2 + 23 + 25 + 27 + 29)
Vậy A : 3.
211. Cho a = 45, b = 204, c = 126.
a. Tìm ƯCLN (a, b, c)
b. Tìm BCNN (a, b)
Giải:
Ta có: 45 = 32.5
204 = 22.3.17
126 = 2.32.7
a. ƯCLN (45; 204; 126) = 3
b. BCNN (45; 204) = 22.32.5.17 = 3060
chia hết cho 9 nên 1 + (*) + 5 + 0 = [6 + (*)] ⋮ 9
Suy ra (*) = 3
Vậy ta có số 1350
Vì 1250 ⋮ 9 nên 1350 ⋮ 3
Vì ƯCLN (2; 3) = 1 nên 1350 ⋮ (2; 3) = 6
Vậy số 1350 chia hết cho tất cả các số 2, 3, 5, 6, 9.
210. Tổng sau có chia hết cho 3 không?
A = 2 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 210
Giải:
Ta có: A = 2 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 210
= (2 + 22) + (23 + 24) + (25 + 26) + (27 + 28) + (29 + 210)
= 2.(1 + 2) + 23.(1 + 2) + 25.(1 + 2) + 27.(1 + 2) + 29.(1 + 2)
= 2.3 + 23 3 + 25.3 + 27.3 + 29.3
= 3.(2 + 23 + 25 + 27 + 29)
Vậy A : 3.
211. Cho a = 45, b = 204, c = 126.
a. Tìm ƯCLN (a, b, c)
b. Tìm BCNN (a, b)
Giải:
Ta có: 45 = 32.5
204 = 22.3.17
126 = 2.32.7
a. ƯCLN (45; 204; 126) = 3
b. BCNN (45; 204) = 22.32.5.17 = 3060
Còn tiếp .....
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.