Giải Sách bài tập Toán 6 chương 2 bài 9: Quy tắc chuyển vế - Luyện tập
2019-10-09T12:55:45-04:00
2019-10-09T12:55:45-04:00
https://sachgiai.com/Toan-hoc/giai-sach-bai-tap-toan-6-chuong-2-bai-9-quy-tac-chuyen-ve-luyen-tap-12373.html
/themes/whitebook/images/no_image.gif
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Thứ tư - 09/10/2019 12:55
Hướng dẫn giải chi tiết: Sách bài tập Toán 6 chương 2 bài 9: Quy tắc chuyển vế - Luyện tập
95. Tìm số nguyên x, biết: 11 - (15 + 11) = x - (25 - 9).
Giải:
11 - (15 + 11) = x - (25 - 9)
11 - 15- 11 = x - 16
-15 = x - 16
-15 + 16 = x
x = 1
96. Tìm số nguyên x, biết:
a. 2 - x = 17 - (-5)
b. x - 12 = (-9) - 15
Giải:
a. 2 - x = 17 - (-5) => 2 – x = 17 + 5=> 2 - x = 22
=> x - 22 = x => x = -22
b. x - 12 = (-9) - 15 => x - 12 = (-9) + (-15) => x - 12 = -24
=> x = -24 + 12 => x = -12
97. Tìm số nguyên a, biết:
a. |a| = 7
b. |a + 6| = 0
Giải:
a. Vì |a| = 7 nên a = 7 hoặc a = -7.
b. Vì |a + 6| = 0 nên a + 6 = 0 => a = -6.
98. a. Viết tổng của ba số nguyên: 14, (-12) và x.
b. Tìm x, biết tổng trên bằng 10.
Giải:
a. Tổng của ba số nguyên: 14, (-12) và x là 14 + (-12) + x
b. Ta có: 14 + (-12) + x = 10 => 2 + x = 10 => x = 10 – 2 => x = 8
99. Cho a, b ϵ ℤ. Tìm số nguyên x, biết:
a. a + x = 7
b. a - x = 25
Giải:
a. Ta có: a + x = 7 => x = 7 - a
b. Ta có: a - x = 25 => a - 25 = x => x = a - 25
100. Cho a, b ϵ ℤ. Tìm số nguyên X, biết:
a. b + x = a
b. b - x = a
Giải:
a. Ta có: b + x = a => x = a - b
b. Ta có: b - x = a => b - a = x => x = b - a
101. Đối với bất đẳng thức, ta cũng có các tính chất sau đây (tương tự như đối với đẳng thức):
Nếu a > b thì a + c > b + c
Nếu a + c > b + c thì a > b
Hãy phát biểu quy tắc chuyển vế trong bất đẳng thức.
Giải:
Quy tắc chuyển vế trong bất đẳng thức: Khi chuyển một số hạng từ vế này sang vế kia của bất đẳng thức, ta phải đổi dấu các số hạng đó, dấu đổi thành dấu và dấu thành dấu.
102. Cho x, y ϵ ℤ. Hãy chứng tỏ rằng:
a. Nếu x - y > 0 thì x > y
b. Nếu x > y thì x - y > 0
Giải:
Áp dụng quy tắc chuyến vế trong bất đẳng thức, ta có:
a. x - y > 0 => x > 0 + y => x > y
b. x > y => x – y > 0
103. Người ta chứng minh được rằng: Khoảng cách giữa hai điểm a, b trên trục số (a, b ϵ ℤ) bằng |a – b| hay |b - a|. Hãy tìm khoảng cách giữa các điểm a và b trên trục số khi:
a. a = -3, b = 5
b. a = 15, b = 37
Giải:
a. Khoảng cách giữa hai điểm a và b trên trục số bằng:
|-3 - 5| = |-3 + (-5)| = |-8| = 8
b. Khoảng cách giữa hai điểm a và b trên trục số bằng:
|15 - 37| = |15 + (-37)| = |-22| = 22
LUYỆN TẬP
104. Tìm số nguyên x, biết: 9 - 25 = (7 - x) - (25 + 7).
Giải:
9 - 25 = (7 - x) - (25 + 7)
9 + (-25) = 7 – x – 25 - 7
-16 = 7 - x - 25 - 7
x = 7- 7 - 25 + 16
x = -25 + 16
x = -9
105. Đội bóng A năm ngoái ghi được 21 bàn và để thủng lưới 32 bàn. Năm nay đội ghi được 35 bàn và để thủng lưới 31 bàn. Tính hiệu số bàn thắng - thua của đội A trong mỗi mùa giải:
a. Năm ngoái
b. Năm nay
Giải:
a. Hiệu số bàn thắng - thua của đội A trong năm ngoái:
21 - 32 = 21 + (-32) = -11 (bàn)
b. Hiệu số bàn thắng - thua của đội A trong năm nay:
35 - 31 = 4 (bàn)
106. Vùng Xi-bê-ri (Liên bang Nga) có nhiệt độ chênh lệch (nhiệt độ cao nhất trừ nhiệt độ thấp nhất) trong năm nhiều nhất thế giới: nhiệt độ thấp nhất là -70°C, nhiệt độ cao nhất là 37°C. Tính nhiệt độ chênh lệch của vùng Xi-bê-ri.
Giải:
Nhiệt độ chênh lệch của vùng Xi-bê-ri:
37 - (-70) = 37 + 70 = 107 (°C)
107. Tính các tổng sau một cách hợp lí:
a. 2575 + 37 - 2576 - 29
b. 34 + 35 + 36 + 37 - 14 - 15 - 16 - 17
Giải:
a. 2575 + 37 - 2576 - 29 = (2575 - 2576) + (37 - 29) = -1 + 8 = 7
b. 34 + 35 + 36 + 37 - 14 - 15 - 16 - 17
= (34 - 14) + (35 - 15) + (36 - 16) + (37 - 17)
= 20 + 20 + 20 + 20 = 80
108. Tính nhanh:
a. -7624 + (1543 + 7624)
b. (27 - 514) - (486 - 73)
Giải:
a. -7624 + (1543 + 7624) = (-7624 + 7624) + 1543 = 1543
b. (27 - 514) - (486 - 73) = 27 - 514 - 486 + 73
= (27 + 73) - (514 + 486) = 100 - 1000 = - 900
109. Đố: Có 9 tấm bìa có ghi số và chia thành 3 nhóm như hình bên dưới. Hãy chuyển một bìa từ một nhóm nào đó sang nhóm khác sao cho tổng các số trong mỗi nhóm đều bằng nhau.
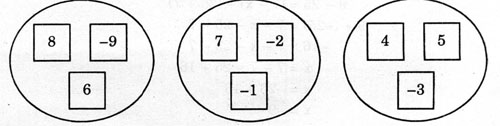 Giải:
Tổng các số trong mỗi nhóm:
- Nhóm thứ nhất: 8 + 6 + (-9) = 14 + (-9) = 5
- Nhóm thứ hai: 7 + (-2) + (-1) = 7 + (-3) = 4
- Nhóm thứ ba: 4 + 5 + (-3) = 9 + (-3) = 6
Tổng của ba nhóm: 5 +4 + 6 = 15
Tổng các số trong mỗi nhóm bằng nhau và bằng: 15 : 3 = 5
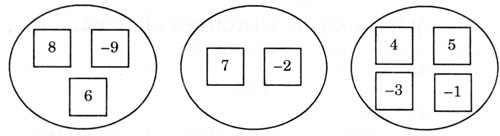
Như vậy, chỉ cần chuyển tấm bảng có ghi số -1 từ nhóm có tổng là 4 sang nhóm có tổng là 6 thì ta được ba nhóm có tổng bằng nhau.
Giải:
Tổng các số trong mỗi nhóm:
- Nhóm thứ nhất: 8 + 6 + (-9) = 14 + (-9) = 5
- Nhóm thứ hai: 7 + (-2) + (-1) = 7 + (-3) = 4
- Nhóm thứ ba: 4 + 5 + (-3) = 9 + (-3) = 6
Tổng của ba nhóm: 5 +4 + 6 = 15
Tổng các số trong mỗi nhóm bằng nhau và bằng: 15 : 3 = 5
Như vậy, chỉ cần chuyển tấm bảng có ghi số -1 từ nhóm có tổng là 4 sang nhóm có tổng là 6 thì ta được ba nhóm có tổng bằng nhau.
 110. Ba người A, B và C chơi một trò chơi tính điểm và tổng số điểm của ba người luôn bằng 0. Hỏi:
a. B được bao nhiêu điểm nếu biết A được 8 điếm và C được -3 điểm?
b. C được bao nhiêu điểm nếu biết trung bình cộng số điểm của A và B là 6 điểm?
Giải:
a. Thay A = 8, C = -3 vào biểu thức A + B + c = 0, ta có:
8 + B + (-3) = 0 => B = -8 + 3 => B = - 5
Vậy B được -5 điểm.
b. Tổng điểm của A và B là: 6 x 2 = 12 (điểm)
Vậy C được -12 điểm.
111. Trò chơi toán học
Trên bảng ghi 20 số từ 1 đến 20 như sau:
110. Ba người A, B và C chơi một trò chơi tính điểm và tổng số điểm của ba người luôn bằng 0. Hỏi:
a. B được bao nhiêu điểm nếu biết A được 8 điếm và C được -3 điểm?
b. C được bao nhiêu điểm nếu biết trung bình cộng số điểm của A và B là 6 điểm?
Giải:
a. Thay A = 8, C = -3 vào biểu thức A + B + c = 0, ta có:
8 + B + (-3) = 0 => B = -8 + 3 => B = - 5
Vậy B được -5 điểm.
b. Tổng điểm của A và B là: 6 x 2 = 12 (điểm)
Vậy C được -12 điểm.
111. Trò chơi toán học
Trên bảng ghi 20 số từ 1 đến 20 như sau:  Hai bạn chơi trò luân phiên điền dấu “+” hoặc “-” vào một ô trống bất kì cho đến khi không còn ô trống nào. Nếu giá trị tuyệt đối của tổng cuối cùng nhỏ hơn 30 thì bạn thứ nhất (đi trước) thắng. Ngược lại, nếu giá trị tuyệt đối của tổng cuối cùng lớn hơn hoặc bằng 30 thì bạn đi sau thắng.
Bạn thứ hai lập luận cho cách đi của mình như sau: Chia 20 số của mình thành 10 cặp (1, 2), (3, 4), ..., (19, 20). Nếu bạn thứ nhất điền dấu vào một số trong mỗi cặp thì bạn thứ hai sẽ điền dâu còn lại của cặp đó theo quy tắc sau: Với cặp (19, 20) bạn ấy sẽ ghi cùng dấu với bạn thứ nhất. Với các cặp còn lại, bạn ấy sẽ ghi khác dấu với bạn đi trước. Hỏi: Với cách đi như vậy, bạn thứ hai (đi sau) có luôn thắng hay không? Giải: thích vì sao?
Giải:
Với cách đi của bạn thứ hai ta thấy có tất cả 10 cặp số, trong đó cặp số (19, 20) có tổng là 39; 9 cặp số còn lại có tổng là -1.
Như vậy tổng của dãy số sẽ là 39 + (-9) = 30.
Vậy bạn thứ hai luôn thắng.
Hai bạn chơi trò luân phiên điền dấu “+” hoặc “-” vào một ô trống bất kì cho đến khi không còn ô trống nào. Nếu giá trị tuyệt đối của tổng cuối cùng nhỏ hơn 30 thì bạn thứ nhất (đi trước) thắng. Ngược lại, nếu giá trị tuyệt đối của tổng cuối cùng lớn hơn hoặc bằng 30 thì bạn đi sau thắng.
Bạn thứ hai lập luận cho cách đi của mình như sau: Chia 20 số của mình thành 10 cặp (1, 2), (3, 4), ..., (19, 20). Nếu bạn thứ nhất điền dấu vào một số trong mỗi cặp thì bạn thứ hai sẽ điền dâu còn lại của cặp đó theo quy tắc sau: Với cặp (19, 20) bạn ấy sẽ ghi cùng dấu với bạn thứ nhất. Với các cặp còn lại, bạn ấy sẽ ghi khác dấu với bạn đi trước. Hỏi: Với cách đi như vậy, bạn thứ hai (đi sau) có luôn thắng hay không? Giải: thích vì sao?
Giải:
Với cách đi của bạn thứ hai ta thấy có tất cả 10 cặp số, trong đó cặp số (19, 20) có tổng là 39; 9 cặp số còn lại có tổng là -1.
Như vậy tổng của dãy số sẽ là 39 + (-9) = 30.
Vậy bạn thứ hai luôn thắng.
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.