Bài 1.
Lấy cột x = -3 làm cột mốc (gọi là cột 1). Vì y là tỉ lệ thuận với x nên ta có thể viết y = kx.
Từ cột thứ tư x = 2, y = -4 ta có: - 4 = k.2
Suy ra k =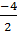 
= -2.
Từ công thức này ta tính được giá trị y trong các cột còn lại.
- Cột thứ nhất: x = -3 thì y = 6
- Cột thứ hai: x = -1 thì y = 2
- Cột thứ ba: x = 1 thì y = -2
- Cột thứ năm: x = 5 thì y = -10
Cuối cùng ta có bảng sau:
| x |
-3 |
-1 |
1 |
2 |
5 |
| y |
6 |
2 |
-2 |
-4 |
-10 |
Nhận xét: Nếu các giá trị phải tìm là y còn các giá trị x đã biết thì ta nên biểu diễn y qua x.
Bài 2.
Vì y tỉ lệ thuận với x nên ta có thể viết y = kx.
Theo cột thứ nhất, ta có: -3,5 = k(-5)
Suy ra k = (-3,5): (-5) = 0,7
Dựa vào công thức này, ta tính được giá trị của y theo x và ngược lại, ta cũng tính được giá trị của x theo y.
Ta lần lượt có:
- Giá trị của y trong cột thứ hai: y = 0,7.(- 3) = - 2,1
- Giá trị của y trong cột thứ ba: y = 0,7.0 = 0
- Giá trị của x trong cột thứ tư: x = y : k = 0,7 : 0,7 = 1
- Giá trị của y trong cột thứ năm: y = 0,7.2 = 1,4
- Giá trị của x trong cột thứ sáu: x = y : k = 2,1 : 0,7 = 3
- Giá trị của x trong cột thứ bảy: x = y : k = 4,2 : 0,7 = 6
Cuối cùng ta có bảng sau:
| x |
-5 |
-3 |
0 |
1 |
2 |
3 |
6 |
| y |
-3,5 |
-2,1 |
0 |
0,7 |
1,4 |
2,1 |
4,2 |
Bài 3.
Ta có bảng:
| t |
-2 |
-1 |
1 |
2 |
3 |
4 |
| s |
60 |
30 |
-30 |
-60 |
-90 |
-120 |
| t |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
b) Vì tỉ số 
không đổi và bằng -
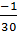nên s và t là hai đại lượng tỉ lệ thuận, s và t được liên hệ với nhau theo công thức t = 
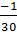s
Hệ số tỉ lệ của t đối với s là t =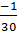 
s
Bài 4.
Vì z tỉ lệ thuận với y theo hệ số tỉ lệ 
nên ta có: z = 
.y (1)
Vì y tỉ lệ thuận với x theo hệ số tỉ lệ 21 nên ta có: y = 21.x (2)
Thay (2) vào (1) ta có: z = 
.21.x => z = 3.x
Vậy z tỉ lệ thuận với x và hệ số tỉ lệ của z đối với x là 3.
Nhận xét: Muốn chứng tỏ z tỉ lệ thuận với x, ta phải đi tìm hệ số k ≠ 0 để z = kx.