Giải vở bài tập Toán 7 chương II bài 2: Một số bài toán về đại lượng tỉ lệ thuận - Luyện tập

Bài 1.
a) Dựa vào bảng ta có:
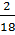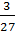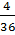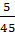 =  =  =  =  =  nên x =  y hay y = 9x
Vậy x và y tỉ lệ thuận với nhau.
b) Vì 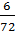 =  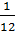≠  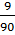=  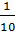nên x và y không tỉ lệ thuận với nhau.

Bài 2.
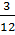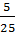a) x và y là hai đại lượng không tỉ lệ thuận với nhau vì:
 =  ≠  =
b) x và y là hai đại lượng không tỉ lệ thuận với nhau vì:
 =  ≠  =

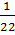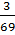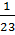Bài 3.
Chú ý đến cùng đơn vị đo
a) Vì khối lượng của cuộn dây thép (y) tỉ lệ thuận vơi chiều dài của nó (x) nên bài ra ta có: y = kx                     (*)
Theo điều kiện: Khi x = 1 (m) thì y = 25 (g).
Thay vào (*) ta tính được k: 25 = k. 1 => k = 25
Vậy công thức biểu diễn y theo x là: y = 25x (đơn vị khối lượng là gam, đơn vị chiều dài là mét)
b) y = 4,5kg = 4500g
Theo câu a) ta có công thức: y = 25x
Nếu y = 4500 (g) thì: 4500 = 25x => x = 4500 : 25 = 180
Vậy cuộn dây dài 180 (m).

Bài 4.
Gọi x là số lít dầu hỏa nặng 12kg. Vì thể tích dầu hỏa và khối lượng dầu hỏa là hai đại lượng tỉ lệ thuận, nên theo tính chất của hai đại lượng tỉ lệ thuận, ta có:
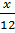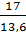 =  => x =  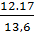= 15
Như vậy, 12kg dầu hỏa có thể tích là 15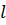 nên hoàn toàn chứa được trong can 16.

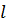Bài 5.
Gọi số tiền lãi chia cho mỗi đơn vị theo thứ tự là x, y, z (triệu đồng). Vì số tiền lãi được chia tỉ lệ với số vốn đóng góp nên theo điều kiện bài ra ta có:
 =   =  và x + y + z = 450
Theo tính chất của dãy tỉ số bằng nhau thì:
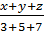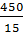 =  =  =  =  = 30
Suy ra: x = 3 . 30 = 90
            y = 5 . 30 = 150
            z = 7 . 30 = 210
Như vậy, số tiền lãi được chia của mỗi đơn vị theo thứ tự là 90, 150, 210 (triệu đồng).
  Bài 1.
Vì khối lượng đường y (kg) tỉ lệ thuận với khối lượng dâu x (kg) để làm mứt dẻo nên ta có: y = kx (k ≠ 0)
Theo điều kiện bài toán, khi y = 3 (kg) thì x = 2 (kg)
Nên ta có: 3 = k.2 suy ra: k =  = 1,5
Vậy công thức biểu thị mối liên hệ giữa lượng đường y và lượng dâu x để làm mứt là: y = l,5x
Khi x = 2,5 (kg) thì y = 1,5.2,5 = 3,75 (kg)
Vậy lượng đường cần để ngâm 2,5kg dâu là 3,75kg
Do đó bạn Hạnh nói dúng.

Bài 2.
Gọi số cây xanh phải trồng và chăm sóc của lớp 7A, 7B, 7C lần lượt là x; y; z.
Theo đề bài ta có:
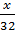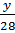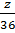 =  =  và x + y + z = 24
Theo tính chất của dãy tỉ số bằng nhau ta có:
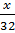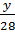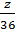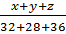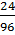 =  =  =  =  = 0,25
Do đó: x = 32.0,25 = 8
            y = 28.0,25 = 7
            z = 36.0,25 = 9
Vậy mỗi lớp 7A, 7B, 7C phải trồng và chăm sóc số cây xanh lần lượt là 8, 7, 9  (cây).

Bài 3.
Gọi lượng niken, kẽm và đồng bạch cần dùng (tính bằng ki-lô-gam) để sản xuất 150 ki-lô-gam đồng bạch lần lượt là x, y, z.
Vì khối lượng mỗi loại tỉ lệ với 3; 4; 13 nên ta có:
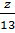 =  =  và x + y + z = 150
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
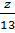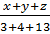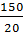 =  =  =  =  = 7,5
Suy ra: x = 3 . 7,5 = 22,5
            y = 4 . 7,5 = 30
            z = 13 . 7,5 = 97,5
Vậy lượng niken, kẽm và đồng dùng sản xuất 150kg đồng bạch lần lượt là 22,5; 30; 97,5 (kg).

Bài 4.
Gọi độ dài các cạnh của tam giác lần lượt là x, y, z. Vì các cạnh của tam giác tỉ lệ với 2; 3; 4 và chu vi của nó là 45cm nên ta có:
 =  =   và x + y + z = 45
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
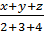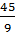 =  =  =  =  = 5 
Suy ra: x = 10
            y = 15
            z = 20
Vậy các cạnh của tam giác lần lượt là 10, 15, 20 (cm)

Bài 5.
Gọi số học sinh giỏi của các khối 6, 7, 8, 9 lần lượt là x, y, z, t.
Theo đề bài, ta có:
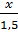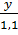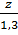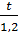 =  =  =  và z – t = 3
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
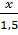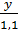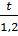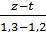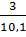 =  =  =  =  =  = 30
Suy ra: x = 1,5 . 30 = 45
            y = 1,1 . 30 = 33
            z = 1,3 . 30 = 39
            t = 1,2 . 30 = 36
Vậy số học sinh giỏi của các khối 6, 7, 8, 9 lần lượt là: 45, 33, 39, 36 (học sinh).