A - Câu hỏi ôn tập chương 1
1. Phát biểu các qui tắc nhân đơn thức với đa thức, nhân đa thức với đa thức.
Trả lời:
- Nhân đơn thức với đa thức: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
- Nhân đa thức với đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
2. Viết bảy hằng đẳng thức đáng nhớ.
Trả lời:
Bảy hằng đẳng thức đáng nhớ:
1) (A + B)2 = A2 + 2AB + B2
2) (A – B)2 = A2 – 2AB + B2
3) A2 – B2 = (A – B)(A + B)
4) (A + B)3 = A3 + 3A2B + 3AB2 + B3
5) (A – B)3 = A3 – 3A2B + 3AB2 – B3
6) A3 + B3 = (A + B)(A2 – AB + B2)
7) A3 – B3 = (A – B)(A2 + AB + B2)
3. Khi nào thì đơn thức A chia hết cho đơn thức B?
Trả lời:
Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
4. Khi nào thì đa thức A chia hết cho đơn thức B?
Trả lời:
Khi từng hạng tử của đa thức A đều chia hết cho đơn thức B thì đa thức A chia hết cho đơn thức B.
5. Khi nào thì đa thức A chia hết cho đa thức B?
Trả lời:
Khi đa thức A chia hết cho đa thức B được dư bằng 0 thì ta nói đa thức A chia hết cho đa thức B.
Bài 75 (trang 33 SGK Toán 8 Tập 1): Làm tính nhân:
a) 5x2.(3x2– 7x + 2)
b) 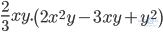
Giải:
a) 5x2.(3x2– 7x + 2)
= 5x2.3x2 – 5x2.7x + 5x2.2
= 15x4 – 35x3 + 10x2
b)
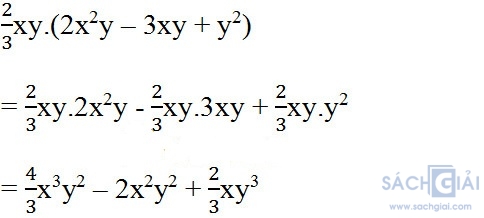
Bài 76 (trang 33 SGK Toán 8 Tập 1): Làm tính nhân:
a) (2x2– 3x)(5x2– 2x + 1) ; b) (x – 2y)(3xy + 5y2 + x)
Giải:
a) (2x2– 3x)(5x2– 2x + 1)
= 2x2.5x2 – 2x2.2x + 2x2 – 3x.5x2 + 3x.2x – 3x
= 10x4 – 4x3 + 2x2 – 15x3 + 6x2 – 3x
= 10x4 – 19x3 + 8x2 – 3x
b) (x – 2y)(3xy + 5y2+ x)
= x.3xy + x.5y2 + x.x – 2y.3xy – 2y.5y2 – 2y.x
= 3x2y + 5xy2 + x2 – 6xy2 – 10y3 – 2xy
= 3x2y – xy2 – 2xy + x2 – 10y3
Bài 77 (trang 33 SGK Toán 8 Tập 1): Tính nhanh giá trị của biểu thức:
a) M = x2+ 4y2– 4xy tại x = 18 và y = 4
b) N = 8x3– 12x2y + 6xy2– y3 tại x = 6 và y = - 8
Giải:
a) M = x2+ 4y2– 4xy
= x2 – 2.x.2y + (2y)2
= (x – 2y)2
Thay x = 18, y = 4 ta được:
M = (18 – 2.4)2 = 102 = 100
b) N = 8x3– 12x2y + 6xy2– y3
= (2x)3 – 3(2x)2y + 3.2xy2 – y3
= (2x – y)3
Thay x = 6, y = - 8 ta được:
N = (2.6 – (-8))3 = 203 = 8000
Bài 78 (trang 33 SGK Toán 8 Tập 1): Rút gọn các biểu thức sau:
a) (x + 2)(x – 2) – (x – 3)(x + 1)
b) (2x + 1)2+ (3x – 1)2+ 2(2x + 1)(3x – 1)
Giải:
a) (x + 2)(x – 2) – (x – 3)(x + 1)
= x2 – 22 – (x2 + x – 3x – 3)
= x2 – 4 – x2 – x + 3x + 3
= 2x – 1
b) (2x + 1)2+ (3x – 1)2+ 2(2x + 1)(3x – 1)
= (2x + 1)2 + 2.(2x + 1)(3x – 1) + (3x – 1)2
= [(2x + 1) + (3x – 1)]2
= (2x + 1 + 3x – 1)2
= (5x)2 = 25x2
Bài 79 (trang 33 SGK Toán 8 Tập 1): Phân tích các đa thức sau thành nhân tử:
a) x2– 4 + (x – 2)2; b) x3 – 2x2 + x – xy2
c) x3– 4x2– 12x + 27
Giải:
a) x2– 4 + (x – 2)2
= (x2– 22) + (x – 2)2
= (x – 2)(x + 2) + (x – 2)2
= (x – 2)[(x + 2) + (x – 2)]
= (x – 2)(x + 2 + x – 2)
= (x – 2)(2x) = 2x(x – 2)
b) x3 – 2x2 + x – xy2
= x(x2 – 2x + 1 – y2)
= x[(x – 1)2 – y2]
= x(x – 1 + y)(x – 1 – y)
c) x3– 4x2– 12x + 27
= (x3 + 27) – (4x2 + 12x)
= (x3 + 33) – 4x(x + 3)
= (x + 3)(x2 – 3x + 9) – 4x(x + 3)
= (x + 3)(x2 – 3x + 9 – 4x)
= (x + 3)(x2 – 7x + 9)
Bài 80 (trang 33 SGK Toán 8 Tập 1): Làm tính chia:
a) (6x3– 7x2– x + 2) : (2x + 1)
b) (x4– x3+ x2 + 3x) : (x2 – 2x + 3)
c) (x2– y2+ 6x + 9) : (x + y + 3)
Giải:

a)
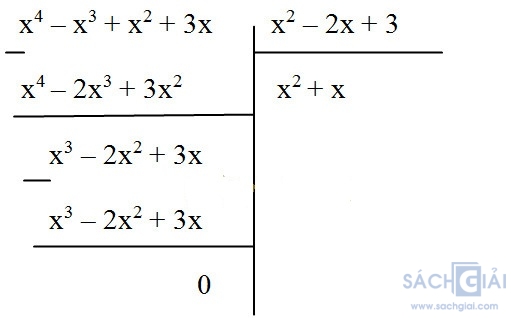
c) (x2– y2+ 6x + 9) : (x + y + 3)
= (x2 + 6x + 9 – y2) : (x + y + 3)
= [(x2 + 2.x.3 + 32) – y2] : (x + y + 3)
= [(x + 3)2 – y2] : (x + y + 3)
= (x + 3 + y)(x + 3 – y) : (x + y + 3)
= x + 3 – y = x – y + 3
Bài 81 (trang 33 SGK Toán 8 Tập 1): Tìm x, biết:
a) 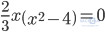
b) (x + 2)2– (x – 2)(x + 2) = 0
c) x + 2√2 x2+ 2x3= 0
Giải:
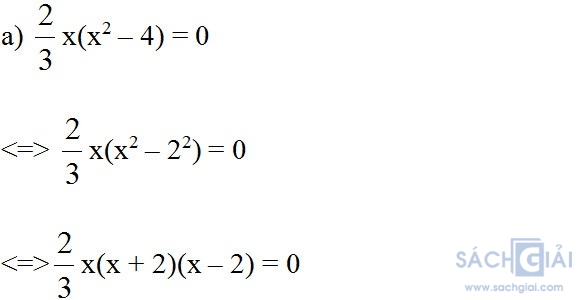
Hoặc x = 0
Hoặc x – 2 = 0 => x = 2
Hoặc x + 2 = 0 => x = - 2
Vậy x = 0; x = - 2; x = 2
b) (x + 2)2– (x – 2)(x + 2) = 0
⇔ (x + 2)[(x + 2) – (x – 2)] = 0
⇔ (x + 2)(x + 2 – x + 2) = 0
⇔ (x + 2).4 = 0
⇔ x + 2 = 0
=> x = - 2
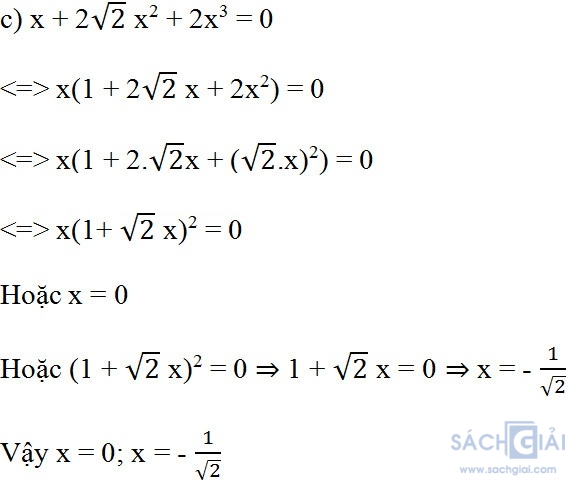
Bài 82 (trang 33 SGK Toán 8 Tập 1): Chứng minh:
a) x2– 2xy + y2+ 1 > 0 với mọi số thực x và y.
b) x – x2– 1 < 0 với mọi số thực x.
Giải:
a) Ta có:
x2 – 2xy + y2 + 1
= (x2 – 2xy + y2) + 1
= (x – y)2 + 1 > 0 do (x – y)2 ≥ 0 với mọi x, y (đpcm).
b) Ta có:
x – x2 – 1 = - (x2 – x + 1)