Mở đầu trang 34: Chúng mình đã biết công thức (a + b)2 = a2 + 2ab + b2, còn công thức tính (a + b)3 thì sao nhỉ?
Giải:
Ta đưa (a + b)
3 về phép nhân đa thức:
(a + b)
3 = (a + b)(a + b)
2.
1. Lập phương của một tổng
Hoạt động 1 trang 34: Với hai số a, b bất kì, thực hiện phép tính (a + b)(a + b)
2. Từ đó rút ra liên hệ giữa (a + b)
3 và a
3 + 3a
2b + 3ab
2 + b
3.
Giải:
Ta có (a + b)(a + b)
2 = (a + b)(a
2 + 2ab + b
2)
= a
3 + 2a
2b + ab
2 + a
2b + 2ab
2 + b
3
= a
3 + (2a
2b + a
2b) + (ab
2 + 2ab
2) + b
3
= a
3 + 3a
2b + 3ab
2 + b
3.
Ta có (a + b)(a + b)
2 = (a + b)
3; (a + b)(a + b)
2 = a
3 + 3a
2b + 3ab
2 + b
3.
Vậy (a + b)3 = a
3 + 3a
2b + 3ab
2 + b
3.
Luyện tập 1 trang 35:
1. Khai triển
a) (x + 3)
3;
b) (x + 2y)
3.
2. Rút gọn biểu thức (2x + y)
3 – 8x
3 – y
3.
Giải:
1.
a) (x + 3)
3 = x
3 + 3 . x
2 . 3 + 3 . x . 3
2 + 3
3 = x
3 + 9x
2 + 27x + 27;
b) (x + 2y)
3 = x
3 + 3 . x
2 . 2y + 3 . x . (2y)
2 + (2y)
3
= x
3 + 6x
2y + 12xy
2 + 8y
3.
2.
(2x + y)
3 – 8x
3 – y
3
= (2x)
3 + 3 . (2x)
2 . y + 3 . 2x . y
2 + y
3 – 8x
3 – y
3
= 8x
3 + 12x
2y + 6xy
2 + y
3 – 8x
3 – y
3
= (8x
3 – 8x
3) + 12x
2y + 6xy
2 + (y
3 – y
3)
= 12x
2y + 6xy
2.
Luyện tập 2 trang 35: Viết biểu thức x3 + 9x2y + 27xy2 + 27y3 dưới dạng lập phương của một tổng.
Giải:
Ta có: x
3 + 9x
2y + 27xy
2 + 27y
3
= x
3 + 3x
2 . 3y + 3 . x . (3y)
2 + (3y)
3
= (x + 3y)
3.
Vậy x
3 + 9x
2y + 27xy
2 + 27y
3 = (x + 3y)
3.
2. Lập phương của một hiệu
Hoạt động 2 trang 35: Với hai số a, b bất kì, viết a – b = a + (–b) và áp dụng hằng đẳng thức lập phương của một tổng để tính (a – b)3.
Từ đó rút ra liên hệ giữa (a – b)3 và a3 – 3a2b + 3ab2 – b3.
Giải:
(a – b)
3 = [a + (–b)]
3 = a
3 + 3a
3(−b) + 3a(−b)
2 + (–b)
3
= a
3 − 3a
2b + 3ab
2 – b
3.
Do đó (a – b)
3 = a
3 – 3a
2b + 3ab
2 – b
3.
Luyện tập 3 trang 35:
Khai triển (2x – y)
3.
Giải:
Ta có (2x – y)
3 = (2x)
3 – 3 . (2x)
2 . y + 3 . 2x . y
2 – y
3
= 8x
3 – 12x
2y + 6xy
2 – y
3.
Luyện tập 4 trang 36: Viết biểu thức dưới dạng lập phương của một hiệu
8x
3 – 36x
2y + 54xy2 – 27y
3.
Giải:
Ta có 8x
3 – 36x
2y + 54xy
2 – 27y
3
= (2x)
3 – 3 . (2x)
2 . 3y + 3 . (2x) . (3y)
2 – (3y)
3
= (2x – 3y)
3.
Vận dụng trang 36: Rút gọn biểu thức: (x – y)3 + (x + y)3.
Giải:
Ta có (x – y)
3 + (x + y)
3
= x
3 – 3x2y + 3xy2 – y
3 + x
3 + 3x2y + 3xy2 + y
3
= (x
3 + x
3) + (3x2y – 3x2y) + (3xy2 + 3xy2) + (y
3 – y
3)
= 2x
3 + 6xy2.
3. Giải bài tập trang 36
Bài 2.7: Khai triển
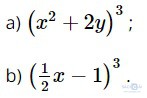 Giải:
Giải:
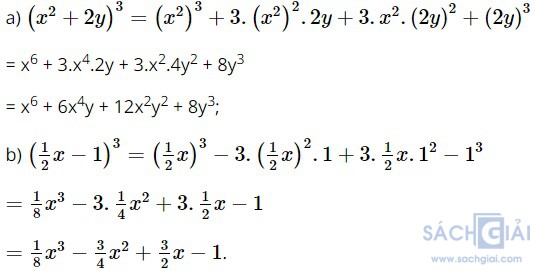 Bài 2.8: Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu.
Bài 2.8: Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu.
a) 27 + 54x + 36x
2 + 8x
3;
b) 64x
3 – 144x
2y + 108xy
2 – 27y
3.
Giải:
a) 27 + 54x + 36x
2 + 8x
3
= 3
3 + 3 . 3
2 . 2x + 3 . 3 . (2x)
2 + (2x)
3
= (3 + 2x)
3;
b) 64x
3 – 144x
2y + 108xy
2 – 27y
3
= (4x)
3 – 3 . (4x)
2 . 3y + 3 . 4x . (3y)
2 – (3y)
3
= (4x – 3y)
3.
Bài 2.9: Tính nhanh giá trị của biểu thức:
a) x
3 + 9x
2 + 27x + 27 tại x = 7;
b) 27 – 54x + 36x
2 – 8x
3 tại x = 6,5.
Giải:
a) Ta có: x
3 + 9x
2 + 27x + 27
= x
3 + 3 . x
2 . 3 + 3 . x . 3
2 + 3
3 = (x + 3)
3.
Thay x = 7 vào biểu thức (x + 3)3, ta được:
(7 + 3)
3 = 10
3 = 1 000.
b) Ta có 27 – 54x + 36x
2 – 8x
3
= 3
3 – 3 . 3
2 . 2x + 3 . 3 . (2x)
2 – (2x)
3
= (3 – 2x)
3.
Thay x = 6,5 vào biểu thức (3 – 2x)
3, ta được:
(3 – 2 . 6,5)
3 = (3 – 13)
3 = (–10)
3 = –1 000.
Bài 2.10: Rút gọn các biểu thức sau:
a) (x – 2y)
3 + (x + 2y)
3;
b) (3x + 2y)
3 + (3x – 2y)
3.
Giải:
a) (x – 2y)
3 + (x + 2y)
3
= x
3 – 3 . x
2 . 2y + 3 . x . (2y)2 – (2y)
3 + x
3 + 3 . x
2 . 2y + 3 . x . (2y)
2 + (2y)
3
= x
3 – 6x
2y + 12xy
2– 8y
3 + x
3 + 6x
2y + 12xy
2+ 8y
3
= (x
3 + x
3) + (6x
2y – 6x
2y) + (12xy
2+ 12xy
2) + (8y
3 – 8y
3)
= 2x
3 + 24xy
2.
b) (3x + 2y)
3 + (3x – 2y)
3
= (3x)
3 + 3 . (3x)
2 . 2y + 3 . 3x . (2y)
2 + (2y)
3 + (3x)
3 – 3 . (3x)
2 . 2y + 3 . 3x . (2y)
2 – (2y)
3
= (3x)
3 + 3 . 3x . (2y)
2 + (3x)
3 + 3 . 3x . (2y)
2
= 27x
3 + 36xy
2 + 27x
3 + 36xy
2
= 54x
3 + 72xy
2.
Bài 2.11: Chứng minh (a – b)3 = – (b – a)3.
Giải:
Ta có
• (a – b)
3 = a
3 – 3a2b + 3ab
2 – b
3;
• – (b – a)
3 = – (b
3 – 3b
2a + 3ba
2 – a
3)
= – b
3 + 3b
2a – 3ba
2 + a
3 = a
3 – 3a
2b + 3ab
2 – b
3.
Vậy (a – b)
3 = – (b – a)
3.