Bài 2.16: Tính nhanh giá trị biểu thức
x
2 +

x +
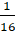
tại x = 99,75
Giải:
Ta có x
2 +

x +
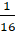
= x
2 + 2. x .

+
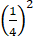
=
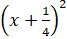
= (x + 0,25)
2
Thay x = 99,75 vào biểu thức (x + 0,25)
2, ta được:
(99,75 + 0,25)
2 = 1002 = 10 000.
Vậy tại x = 99,75 thì giá trị của biểu thức đã cho bằng 10 000.
Bài 2.17: Chứng minh đẳng thức (10a + 5)2 = 100a(a + 1) + 25. Từ đó em hãy nêu một quy tắc tính nhẩm bình phương của một số có tận cùng là 5.
Áp dụng: Tính 252; 352.
Giải:
Ta có (10a + 5)
2 = (10a)
2 + 2 . 10a . 5 + 5
2
= 100a
2 + 100a + 25 = 100a(a + 1) + 25.
Từ đó ta rút ra quy tắc tính nhẩm bình phương của một số có tận cùng là 5 là:
Bình phương của một số tự nhiên có chữ số tận cùng là 5 bằng 100 lần tích của số tạo bởi các chữ số trước số tận cùng với số liền sau của số tạo bởi các chữ số trước số tận cùng rồi cộng với 25.
Áp dụng:
• 252 = (10 . 2 + 5)
2 = 100 . 2 . (2 + 1) + 25 = 100 . 2 . 3 + 25
= 600 + 25 = 625;
• 352 = (10 . 3 + 5)
2 = 100 . 3 . (3 + 1) + 25 = 100 . 3 . 4 + 25
= 1 200 + 25 = 1 225.
Bài 2.18: Tính nhanh giá trị của các biểu thức:
a) x
3 + 3x
2 + 3x + 1 tại x = 99;
b) x
3 – 3x
2y + 3xy
2 – y
3 tại x = 88 và y = –12.
Giải:
a) Ta có x
3 + 3x
2 + 3x + 1
= x
3 + 3 . x
2 . 1 + 3 . x . 1
2 + 1
3 = (x + 1)
3.
Thay x = 99 vào biểu thức (x + 1)3, ta được:
(99 + 1)
3 = 1003 = 1 000 000.
b) Ta có x
3 – 3x
2y + 3xy
2 – y
3 = (x – y)
3.
Thay x = 88 và y = –12 vào biểu thức (x – y)
3, ta được:
[88 – (–12)]
3 = (88 + 12)
3 = 100
3 = 1 000 000.
Bài 2.19: Rút gọn các biểu thức:
a) (x – 2)
3 + (x + 2)
3 – 6x(x + 2)(x – 2);
b) (2x – y)
3 + (2x + y)
3.
Giải:
a) (x – 2)
3 + (x + 2)
3 – 6x(x + 2)(x – 2)
= [(x – 2) + (x + 2)] . [(x – 2)2 – (x – 2).(x + 2) + (x + 2)
2] – 6x(x
2 – 4)
= (x – 2 + x + 2).[x
2 – 4x + 4 – (x
2 – 4) + x
2 + 4x + 4] – 6x(x
2 – 4)
= 2x.(2x
2 + 8 – x
2 + 4) – 6x(x
2 – 4)
= 2x(x
2 + 12) – 6x(x
2 – 4)
= 2x
3 + 24x – 6x
3 + 24x
= – 4x
3 + 48x.
b) (2x – y)
3 + (2x + y)
3
= (2x)
3 – 3 . (2x)2 . y + 3 . 2x . y
2 – y
3 + (2x)
3 + 3 . (2x)
2 . y + 3 . 2x . y
2 + y
3
= (2x)
3 + 3 . 2x . y
2 + (2x)
3 + 3 . 2x . y
2
= 8x
3 + 6xy
2 + 8x
3 + 6xy
2 = 16x
3 + 12xy
2.
Bài 2.20: Chứng minh rằng a3 + b3 = (a + b)3 – 3ab(a + b).
Áp dụng, tính a
3 + b
3 biết a + b = 4 và ab = 3.
Giải:
Ta có (a + b)
3 = a
3 + 3a
2b + 3ab
2 + b
3
= a
3 + 3ab(a + b) + b
3
Do đó a
3 + b
3 = (a + b)
3 – 3ab(a + b).
Áp dụng:
Với a + b = 4 và ab = 3, ta được:
a
3 + b
3 = (a + b)
3 – 3ab(a + b)
= 4
3 – 3 . 3 . 4 = 64 – 36 = 28.
Bài 2.21: Bác Tùng gửi vào ngân hàng 200 triệu đồng theo thể thức lãi kép theo định kì với lãi suất x mỗi năm (tức là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp). Biểu thức S = 200(1+x)3 (triệu đồng) là số tiền bác Tùng nhận được sau 3 năm.
a) Tính số tiền bác Tùng nhận được sau 3 năm khi lãi suất x = 5,5%
b) Khai triển S thành đa thức theo x và xác định bậc của đa thức.
Giải:
a) Số tiền bác Tùng nhận được sau 3 năm khi lãi suất x = 5,5% là:
200 (1 + 0,055)
3 = 234,8483 (triệu đồng)
b) S = 200 (1+x)
3 = 200 (1 + 3x + 3x
2 + x
3)
=200 + 600x + 600x
2 + 200x
3
Đa thức S bậc 3