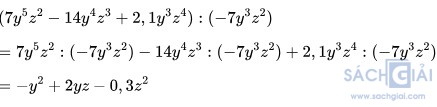1. Chia đơn thức cho đơn thức
Hoạt động 1 trang 22: Hãy nhớ lại cách chia đơn thức cho đơn thức trong trường hợp chúng có một biến và hoàn thành các yêu cầu sau:
a) Thực hiện phép chia 6x
3 : 3x
2.
b) Với a, b ∈ ℝ và b ≠ 0; m, n ∈ ℕ, hãy cho biết:
• Khi nào thì ax
m chia hết cho bx
n.
• Nhắc lại cách thực hiện phép chia axm cho bxn.
Giải:
a) Ta có 6x
3 : 3x
2 = (6: 3)(x
3 : x
2) = 2x.
b) Với a, b ∈ ℝ và b ≠ 0; m, n ∈ ℕ, ta có:
• ax
m chia hết cho bx
n khi m ≥ n.
• Thực hiện phép chia: ax
m : bx
n = (a : b) . (xm : xn) =
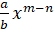 Hoạt động 2 trang 23: Với mỗi trường hợp sau, hãy đoán xem đơn thức A có chia hết cho đơn thức B không, nếu chia hết, hãy tìm thương của phép chia A cho B và giải thích cách làm
Hoạt động 2 trang 23: Với mỗi trường hợp sau, hãy đoán xem đơn thức A có chia hết cho đơn thức B không, nếu chia hết, hãy tìm thương của phép chia A cho B và giải thích cách làm
a) A = 6x
3y, B = 3x
2y;
b) A = x
2y, B = xy
2.
Giải:
a) Dự đoán: Đơn thức A chia hết cho đơn thức B.
Ta có: A : B = 6x
3y : 3x
2y = (6 : 3)(x
3 : x
2)(y : y)
= 2 . x . 1 = 2x.
b) Dự đoán: Đơn thức A không chia hết cho đơn thức B.
A : B = (x
2 : x)(y : y
2) (đơn thức A không chia hết cho đơn thức B)
Đơn thức A không chia hết cho đơn thức B vì trong A có y không chia hết cho y
2 trong B.
Luyện tập 1 trang 23: Trong các phép chia sau đây, phép chia nào không là phép chia hết? Tại sao? Tìm thương của các phép chia còn lại
a) −15x
2y
2 chia cho 3x
2y;
b) 6xy chia cho 2yz;
c) 4xy
3 chia cho 6xy
2.
Giải:
Phép chia 6xy chia cho 2yz không là phép chia hết vì số mũ của biến z trong đơn thức 6xy nhỏ hơn số mũ của biến z trong đơn thức 2yz.
a) Ta có: −15x
2y
2 : 3x
2y = (−15 : 3)(x
2 : x
2)(y
2 : y) = −5y.
Vậy thương của −15x
2y
2 chia cho 3x
2y là −5y.
c) Ta có: 4xy
3 : 6xy
2 = (4 : 6) (x : x) (y
3 : y
2) =

y
Vậy thương của 4xy
3 chia cho 6xy
2 là

y
Vận dụng 1 trang 23: Giải bài toán mở đầu.
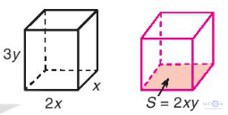
Cho hai khối hộp chữ nhật: khối hộp thứ nhất có ba kích thước x, 2x và 3y; khối hộp thứ hai có diện tích đáy là 2xy. Tính chiều cao (cạnh bên) của khối hộp thứ hai, biết rằng hai khối hộp có cùng thể tích.
 Giải:
Giải:
Thể tích của khối hộp thứ nhất là: 2x . x . 3y = 6x
2y
Vì hai khối hộp có cùng thể tích nên khối hộp thứ hai có thể tích 6x
2y.
Chiều cao của khối hộp thứ hai là: 6x
2y : 2xy = 3x.
Vậy chiều cao (cạnh bên) của khối hộp thứ hai là 3x.
2. Chia đa thức cho đơn thức
Luyện tập 2 trang 24: Làm tính chia (6x4y3 – 8x3y4 + 3x2y2) : 2xy2.
Giải:
Ta có (6x
4y
3 – 8x
3y
4 + 3x
2y
2) : 2xy
2
= 6x
4y
3 : 2xy
2 – 8x3y
4 : 2xy
2 + 3x
2y
2 : 2xy
2
= 3x
3y – 4x
2y
2 +

x
Vận dụng 2 trang 24: Tìm đa thức A sao cho A . (−3xy) = 9x3y + 3xy3 – 6x2y2.
Giải:
Ta có A . (−3xy) = 9x3y + 3xy
3 – 6x
2y
2.
Suy ra A = (9x
3y + 3xy
3 – 6x
2y
2) : (−3xy)
= 9x
3y : (−3xy) + 3xy
3 : (−3xy) – 6x
2y
2 : (−3xy)
= −3x
2 − y
2 + 2xy.
3. Giải bài tập trang 24
Bài 1.30:
a) Tìm đơn thức M, biết rằng  x3y2 : M = 7xy2
x3y2 : M = 7xy2
b) Tìm đơn thức N sao cho N : 0,5xy2z = −xy.
Giải:
a) Ta có

x
3y
2 : M = 7xy
2
Suy ra M =

x
3y
2 : 7xy
2 =
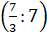
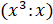 (y2 : y2)
(y2 : y2)
Vậy M =

x
2
b) Ta có N : 0,5xy
2z = −xy
Suy ra N = −xy . 0,5xy2z = −0,5(x . x)(y . y
2)z = −0,5x
2y
3z.
Vậy N = −0,5x
2y
3z.
Bài tập 1.31 trang 24: Cho đa thức A = 9xy4 – 12x2y3 + 6x3y2. Với mỗi trường hợp sau đây, xét xem A có chia hết cho đơn thức B hay không? Thực hiện phép chia trong trường hợp A chia hết cho B.
a) B = 3x
2y;
b) B = −3xy
2.
Giải:
a) Đa thức A = 9xy
4 – 12x
2y
3 + 6x
3y
2 không chia hết cho đơn thức B = 3x
2y vì đơn thức 9xy
4 không chia hết cho 3x
2y.
Do đó, đa thức A = 9xy
4 – 12x
2y
3 + 6x
3y
2 không chia hết cho đơn thức B = 3x
2y.
b) Đa thức A = 9xy
4 – 12x
2y
3 + 6x
3y
2 chia hết cho đơn thức B = −3xy
2.
Ta có: A : B = 9xy
4 : (−3xy
2) – 12x
2y
3 : (−3xy
2) + 6x
3y
2 : (−3xy
2)
= −3y
2 + 4xy − 2x
2.
Bài 1.32: Thực hiện phép chia  Giải:
Giải: