Phần trắc nghiệm (3 điểm)
Câu 1:Điều kiện để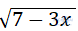 
có nghĩa là:
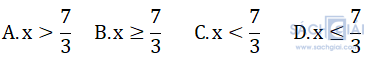
Câu 2: So sánh 5 với 2√6 ta có kết luận:
A.5 > 2√6 B.5 < 2√6
C.5 = 2√6 D.Không so sánh được
Câu 3: Biểu thức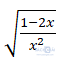 
xác định khi:
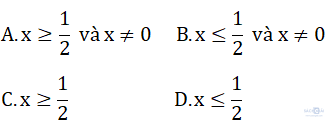
Câu 4: Phương trình √x = a vô nghiệm khi
A.a > 0 B.a = 0 C.a < 0 D.Mọi a
Câu 5: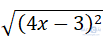 
bằng:
A.4x - 3 B.-(4x - 3) C.-4x + 3 D.|4x - 3|
Câu 6:Giá trị của biểu thức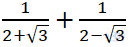 
bằng:
A.-2√3 B.4 C.0 D.1/2
Phần tự luận (7 điểm)
Bài 1. (2 điểm) Thực hiện các phép tính:
a) (15√50 + 5√200 - 3√450):√10
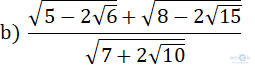
Bài 2. (2 điểm)a) Tìm x biết:
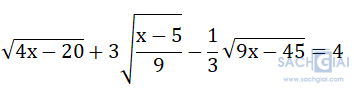
b) Rút gọn
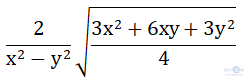
Bài 3. (2,5 điểm) Cho biểu thức:
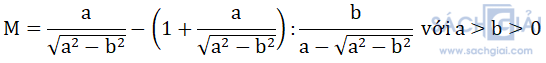
a) Rút gọn M.
b) Tính giá trị M nếu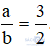 
c) Tìm điều kiện của a, b để M < 1.
Bài 4. (0,5 điểm) Tìm giá trị lớn nhất của biểu thức :
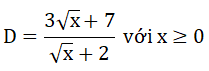
GIẢI
Phần trắc nghiệm (3 điểm)
| 1. D | 2. A | 3. B | 4. C | 5. D | 6. B |
Phần tự luận (7 điểm)
Bài 1. (2 điểm) Thực hiện các phép tính:
a) (15√50 + 5√200 - 3√450) : √10
= 15√5 + 5√20 - 3√45
= 15√5 + 10√5 - 9√5
= 16√5
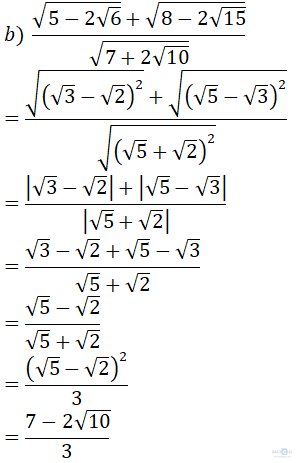
Bài 2. (2 điểm)
a) ĐKXĐ: x ≥ 5
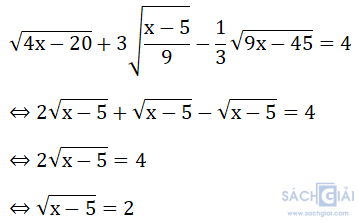
⇔ x - 5 = 4
⇔ x = 9 (Thỏa mãn ĐKXĐ)
b) Với x > 0; y > 0
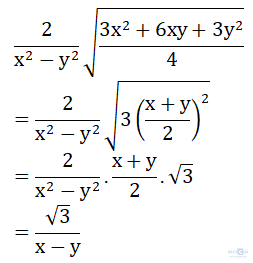
Bài 3.
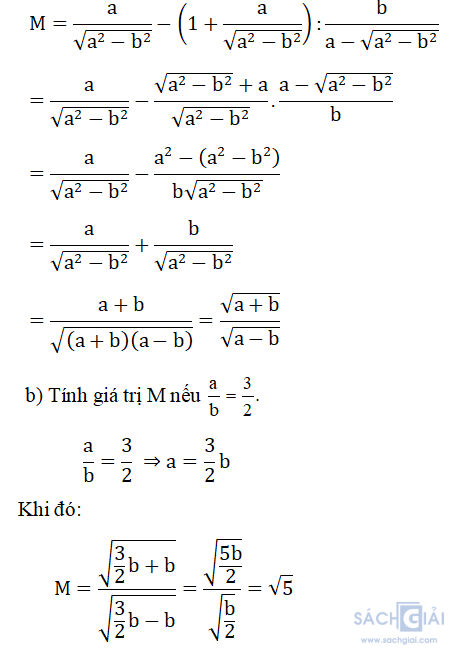
c) Tìm điều kiện của a, b để M < 1
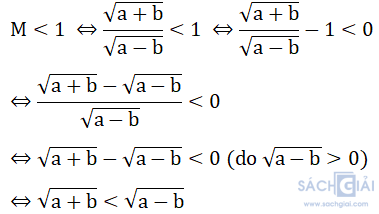
⇔ a + b < a-b
⇔ b < 0
Vô lí do a > b > 0
Vậy không tồn tại a, b sao cho M < 1
Bài 4.
Với x ≥ 0,ta có:
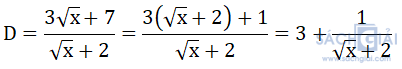
D lớn nhất ⇔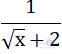 
⇔ √x + 2 nhỏ nhất
Mà √x + 2 ≥ 2 ∀x > 0
Vậy maxD = 3 + 1/2 = 7/2 ⇔ x = 0