Phần trắc nghiệm (3 điểm)
Câu 1: Số có căn bậc hai số học của nó bằng 9 là:
A. -3 B. 3 C. -81 D.81
Câu 2: Biểu thức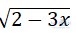 
xác định với giá trị:
Câu 3: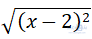 
sau khi bỏ dấu căn, kết quả là:
A.x - 2 B.2 - x C.2 - x và x - 2 D.|x - 2|
Câu 4: Giá trị của biểu thức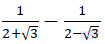 
bằng:
A.-2√3 B.2√3 C.4 D.1
Câu 5: Giá trị của biểu thức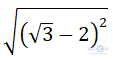 
bằng:
A.1 B.√3 - 2 C. 2 - √3 D. √5
Câu 6: Rút gọn biểu thức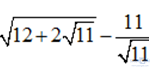 
được kết quả là:
A.-1 B.1 C.-11 D.11
Phần tự luận (7 điểm)
Bài 1. (2 điểm) Thực hiện phép tính:
Bài 2. (2 điểm)
a) Tính giá trị biểu thức:
b) Với x > 0, x ≠ 4 và x ≠ 9. Hãy chứng tỏ rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x
Bài 3. (2,5 điểm) Cho biểu thức:
a) Rút gọn A.
b) Tìm a để A < 0
Bài 4. (0,5 điểm) Chứng minh rằng không tồn tại một tam giác có độ dài ba đường cao là 1; √3; √3 + 1 ( cùng đơn vị đo).
GIẢI
Phần trắc nghiệm (3 điểm)
Phần tự luận (7 điểm)
Bài 1. Thực hiện các phép tính:
= |3 + √2| - |3 - √2|
= 3 + √2 - 3 + √2
= 2√2
Bài 2.
b) Với x > 0; x ≠ 4; x ≠ 9 ta có:
Vậy giá trị của B không phụ thuộc vào giá trị của biến x
Bài 3.
Bài 4.
Giả sử tồn tại một tam giác có độ dài các đường cao là : h1 = 1; h2 = √3; h3 = 1 + √3 (cùng đơn vị đo )
Gọi a1; a2; a3 lần lượt là độ dài ba cạnh tương ứng với các đường cao h1; h2 ; h3 .
Ta có: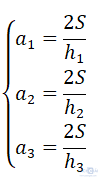 
a1; a2; a3 lần lượt là 3 cạnh của tam giác nên:
Vậy không tồn tại một tam giác có độ dài 3 đường cao lần lượt là 1; √3; 1 + √3 (cùng đơn vị đo)