Giải Sách bài tập Toán 6 bài 8: Chia hai lũy thừa cùng cơ số
2019-10-06T12:59:48-04:00
2019-10-06T12:59:48-04:00
https://sachgiai.com/Toan-hoc/giai-sach-bai-tap-toan-6-bai-8-chia-hai-luy-thua-cung-co-so-12343.html
/themes/whitebook/images/no_image.gif
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Chủ nhật - 06/10/2019 12:58
Hướng dẫn giải chi tiết: Sách bài tập Toán 6 - Bài 8: Chia hai lũy thừa cùng cơ số
96. Viết kết quả phép tính dưới dạng một lũy thừa:
a. 56 : 53
b. a4 : a (a ≠ 0)
Giải:
a. 56 : 53 = 56-3 = 53 b. a4 : a = a4’1 = a3 (a ≠ 0)
97. Viết các số 895 và 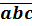 dưới dạng tổng các lũy thừa của 10.
Giải:
895 = 8.100 + 9.10 + 5.1 = 8.102 + 9.101 + 5.100
dưới dạng tổng các lũy thừa của 10.
Giải:
895 = 8.100 + 9.10 + 5.1 = 8.102 + 9.101 + 5.100
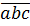 = a.100 + b.10 + c.l = a.102 + b.101 + c.100
98. Tìm số tự nhiên a, biết rằng với mọi n ∈ N ta có an = 1
Giải:
* Nếu n ≠ 0 ta có: an =
= a.100 + b.10 + c.l = a.102 + b.101 + c.100
98. Tìm số tự nhiên a, biết rằng với mọi n ∈ N ta có an = 1
Giải:
* Nếu n ≠ 0 ta có: an = 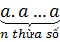 . Mà an = 1 suy ra a = 1
* Nếu n = 0 ta có: an = a0. Mà an = 1 suy ra a ∈ N*
Vậy nếu n ≠ 0 thì a = 1, n = 0 thì a ∈ N*
99. Mỗi tổng sau có là một số chính phương không?
a. 32 + 42
b. 52 + 122
Giải:
a. 32 + 42 = 3.3 + 4.4 = 9 + 16 = 25 = 52
. Mà an = 1 suy ra a = 1
* Nếu n = 0 ta có: an = a0. Mà an = 1 suy ra a ∈ N*
Vậy nếu n ≠ 0 thì a = 1, n = 0 thì a ∈ N*
99. Mỗi tổng sau có là một số chính phương không?
a. 32 + 42
b. 52 + 122
Giải:
a. 32 + 42 = 3.3 + 4.4 = 9 + 16 = 25 = 52
Vậy 32 + 42 là số chính phương.
b. 52 + 122 = 5.5 + 12.12 = 25 + 144 = 169 = 132
Vậy 52 + 122 là số chính phương.
100. Viết kết quả phép tính dưới dạng một lũy thừa:
a. 315 : 35
b. 46 : 46
c. 98 : 32
Giải:
a. 315 : 35 = 315-5 = 310
b. 46 : 46 = 46-6 = 40
c. 98 : 32 = 98 : 9 = 98-1 = 97
101. a. Vì sao số chính phương không tận cùng bằng các chữ số 2, 3, 7, 8?
b. Tổng (hiệu) sau có là số chính phương không?
3.5.7.9.11 + 3;
2.3.4.5.6 - 3
Giải:
a. Số chính phương là số bằng bình phương đúng của một số tự nhiên. Theo đó, ta có bảng dưới đây:
| Tận cùng của m |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| Tận cùng của m2 |
0 |
1 |
4 |
9 |
6 |
5 |
6 |
9 |
4 |
1 |
Từ kết quả trên, ta thấy số chính phương không thể tận cùng bằng các chữ số 2, 3, 7, 8.
b. 3.5.7.9.11 + 3 = 10395 + 3 = 10398
Số tận cùng là 8 nên tổng trên không phải là số chính phương.
2.3.4.5.6 - 3 = 720 - 3 = 717
Số tận cùng là 7 nên hiệu trên không phải là số chính phương.
102. Tìm số tự nhiên n, biết rằng:
a. 2n = 16
b. 4n = 64
c. 15n = 225
Giải:
a. Ta có: 16 = 24. Suy ra: 2n = 24. Vậy n = 4.
b. Ta có: 64 = 43. Suy ra: 4n = 43. Vậy n = 3.
c. Ta có: 225 = 152. Suy ra: 15n = 152. Vậy n = 2.
103. Tìm số tự nhiên x mà x50 = x.
Giải:
Ta có: x50 = 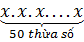 Mà x50 = x nên chỉ có hai giá trị của x thỏa là x = 0 và x = 1.
Mà x50 = x nên chỉ có hai giá trị của x thỏa là x = 0 và x = 1.
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.