Loading...

Giải Sách bài tập Toán 6 bài 10: Tính chất chia hết của một tổng

Thứ hai - 07/10/2019 04:12

Hướng dẫn giải chi tiết: Sách bài tập Toán 6 - Bài 10: Tính chất chia hết của một tổng

Loading...
114. Áp dụng tính chất chia hết, xét xem mỗi tổng (hiệu) sau có chia hết cho 6 không?
a. 42 + 54
b. 600 - 14
c. 120 + 48 + 20
d. 60 + 15 + 3
Giải:
a. Vì 42 ⁞ 6 và 54 ⁞ nên (42 + 54) ⁞ 6
b. Vì 600 ⁞ 6 nhưng 14 không chia hết cho 6 nên (600 - 14) không chia hết cho 6
c. Vì 120 ⁞ 6, 48 ⁞ 6 nhưng 20 không chia hết cho 6 nên (120 + 48 + 20) không chia hết cho 6
d. Vì 60 ⁞ 6 và 15 + 3 = 18 ⁞ 6 nên (60 + 15 + 3) ⁞ 6

115. Cho tổng A = 12 + 15 + 21 + x, với x 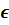 N. Tìm điều kiện của x để A chia hết cho 3, để A không chia hết cho 3.
Giải:
Ta có: 12 ⁞ 3; 15 ⁞ 3; 21 ⁞ 3
Suy ra: A = (12 + 15 + 21 + x) ⁞ 3 khi x ⁞ 3
A = (12 + 15 + 21 + x) không chia hết cho 3 khi x không chia hết cho 3.

116. Khi chia số tự nhiên a cho 24, ta được số dư là 10. Hỏi số a có chia hết cho 2 không? Có chia hết cho 4 không?
Giải:
Ta có: a = 24k + 10 (k ∈ N)
Vì 24 ⁞ 2 và 10 ⁞ 2 nên (24k + 10) ⁞ 2
Vì 24 ⁞ 4 và 10 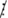 4 nên (24k + 10)  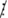4

117. Điền dấu “x” vào ô thích hợp:
Câu Đúng Sai
Nếu mỗi số hạng của tổng không chia hết cho 4 thì tổng không chia hết cho 4    
Nếu tổng của hai số chia hết cho 3, một trong hai số chia hết cho 3 thì số còn lại chia hết cho 3    

Giải:
Câu Đúng Sai
Nếu mỗi số hạng của tổng không chia hết cho 4 thì tổng không chia hết cho 4   x
Nếu tổng của hai số chia hết cho 3, một trong hai số chia hết cho 3 thì số còn lại chia hết cho 3 x  

118. Chứng tỏ rằng:
a. Trong hai số tự nhiên liên tiếp, có một số chia hết cho 2.
b. Trong ba số tự nhiên liên tiếp, có một số chia hết cho 3.
Giải:
a. Gọi hai số tự nhiên liên tiếp là a và a + 1
Nếu a chia hết cho 2 thì bài toán được chứng minh.
Nếu a không chia hết cho 2 thì a = 2k + 1 (k ∈ N)
Suy ra: a + 1 = 2k + 1 + 1
Ta có: 2k ⁞ 2; 1 + 1 = 2 ⁞ 2
Suy ra: (2k + 1 + 1) ⁞ 2 hay (a + 1) ⁞ 2
Vậy trong hai số tự nhiên liên tiếp, có một số chia hết cho 2.
b. Gọi ba số tự nhiên liên tiếp là a, a + 1 và a + 2
Nếu a chia hết cho 3 thì bài toán được chứng minh.
Nếu a không chia hết cho 3 thì a = 3k + 1 hoặc a = 3k + 2 (k ∈ N)
Nếu a = 3k + 1 thì a + 2 = 3k + l+ 2 = 3k + 3 ⁞ 3
Nếu a = 3k + 2 thì a + l = 3k + 2 + l = 3k + 3 ⁞ 3
Vậy trong ba số tự nhiên liên tiếp, có một số chia hết cho 3.

119. Chứng tỏ rằng:
a. Tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3.
b. Tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4.
Giải
a. Gọi ba số tự nhiên liên tiếp là a, a + 1 và a + 2
Ta có: a + (a + 1) + (a + 2) = (a + a + a) + (1 + 2) = 3a + 3
Vì 3 ⁞ 3 nên 3a ⁞ 3, suy ra (3a + 3) ⁞ 3
Vậy tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3.
b. Gọi bốn số tự nhiên liên tiếp là a, a + 1, a + 2 và a + 3
Ta có: a + (a + 1) + (a + 2) + (a + 3)
= (a + a + a + a) + (1 + 2 + 3) = 4a + 6
Vì 4 ⁞ 4 nên 4a ⁞ 4 nhưng 6 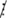 4, suy ra (4a + 6) 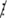4
Vậy [a + (a + 1) + (a + 2) + (a + 3)] 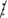 4

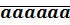120. Chứng tỏ rằng số có dạng  bao giờ cũng chia hết cho 7 (chẳng hạn: 333333 ⁞ 7).
Giải:
Ta có: 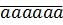  = 111111.a = 3.7.11.13.37.a
Vì 3.7.11.13.37.a : 7 nên 111111.a ⁞ 7.
Vậy số có dạng   bao giờ cũng chia hết cho 7.

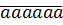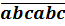121. Chứng tỏ rằng số có dạng  bao giờ cũng chia hết cho 11 (chẳng hạn: 328328 ⁞ 11).
Giải:
Ta có: 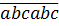 = 1001.  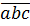= 7.11.13.
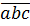Vì 7.11.13. 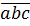⁞ 11 nên 1001. 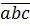⁞ 11
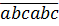Vậy số có dạng  bao giờ cũng chia hết cho 11.

122. Chứng tỏ rằng lấy một số có hai chữ số, cộng với số gồm hai chữ số ấy viết theo thứ tự ngược lại, ta luôn luôn được một số chia hết cho 11 (chẳng hạn 37 + 73 = 110, chia hết cho 11).
Giải
Gọi số tự nhiên có hai chữ số là 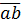 (a ≠ 0)
Số viết theo thứ tự ngược lại củ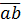a  là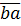
Số ab viết dưới dạng tổng các hàng đơn vị là 10a + b
Số ba viết dưới dạng tổng các hàng đơn vị là 10b + a
Ta có: 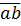 +  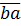= (10a + b) + (10b + a) = 11a + 11b = 11.(a + b)
Vì 11.(a + b) : 11 nên ab + ba luôn chia hết cho 11.
Bản quyền bài viết thuộc về Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.
Loading...

Tổng số điểm của bài viết là: 0 trong 0 đánh giá

Click để đánh giá bài viết

  Ý kiến bạn đọc

Mã bảo mật   

Theo dòng sự kiện

Xem tiếp...

Những tin mới hơn

Những tin cũ hơn

Loading...
GIẢI BÀI TẬP
Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5
Lớp 6 Lớp 7 Lớp 8 Lớp 9
Lớp 10 Lớp 11 Lớp 12
Trung cấp Cao đẳng Đại học
Bài soạn Kể chuyện Tiểu sử
Bài kiểm tra Bài làm văn
Viết thư UPU Bài hướng dẫn
Vượt khó học giỏi Người tốt việc tốt
Phương pháp dạy Phương pháp học
SÁCH GIẢI
Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5
Lớp 6 Lớp 7 Lớp 8 Lớp 9
Lớp 10 Lớp 11 Lớp 12
THPT Trẻ em Người lớn
Truyện ngắn Truyện dài Tiểu thuyết Cổ tích Võ thuật
SÁCH MỚI
Hướng dẫn trả lời câu hỏi và bài tập Địa lí 11 Hướng dẫn trả lời câu hỏi và bài tập Địa lí 11
Hướng dẫn học Khoa học - Lịch sử - Địa lí 5 Hướng dẫn học Khoa học - Lịch sử - Địa lí 5
Giải vở bài tập Toán 7 - Tập 1 Giải vở bài tập Toán 7 - Tập 1
Công nghệ 9 - Lắp đặt mạng điện trong nhà Công nghệ 9 - Lắp đặt mạng điện trong nhà
Công nghệ 7 - Nông nghiệp Công nghệ 7 - Nông nghiệp
Công nghệ 6 - Kinh tế gia đình Công nghệ 6 - Kinh tế gia đình
Bạn đã không sử dụng Site, Bấm vào đây để duy trì trạng thái đăng nhập. Thời gian chờ: 60 giây