Học tốt Vật lí 12 bài 3: Con lắc đơn
2019-08-08T08:34:25-04:00
2019-08-08T08:34:25-04:00
https://sachgiai.com/Vat-ly/hoc-tot-vat-li-12-bai-3-con-lac-don-11849.html
/themes/whitebook/images/no_image.gif
Sách Giải
https://sachgiai.com/uploads/sach-giai-com-logo.png
Thứ ba - 06/08/2019 10:04
Hệ thống kiến thức lí thuyết cơ bản cần nhớ, hướng dẫn trả lời câu hỏi sách giáo khoa và giải bài tập Vật lí 12, Bài 3: Con lắc đơn
A. Kiến thức cơ bản
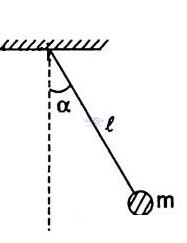
1. Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu một sợ dây không dãn, khối lượng không đáng kể, dài l.
 2. Chu kì - tần số - tần số góc
Khi con lắc đơn dao động nhỏ (với since α = α (rad)), con lắc đơn dao động điều hòa theo phương trình s = s0cos(ωt + φ), trong đó: s0= lα0 là biên độ dao động. Với.
- Chu kì: T = 2π
2. Chu kì - tần số - tần số góc
Khi con lắc đơn dao động nhỏ (với since α = α (rad)), con lắc đơn dao động điều hòa theo phương trình s = s0cos(ωt + φ), trong đó: s0= lα0 là biên độ dao động. Với.
- Chu kì: T = 2π Với:
l: chiều dài con lắc (m)
g: gia tốc trọng trường (m/s2)
T: chu kì con lắc đơn (s)
- Tần số f =
Với:
l: chiều dài con lắc (m)
g: gia tốc trọng trường (m/s2)
T: chu kì con lắc đơn (s)
- Tần số f =  =
= 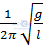 - Tần số góc: ω =
- Tần số góc: ω = 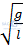 3. Động năng - thế năng - cơ năng của con lắc đơn
Động năng: Wđ=
3. Động năng - thế năng - cơ năng của con lắc đơn
Động năng: Wđ=  mv2
Thế năng: Wt= mgl (1 - cosα)
Cơ năng: Nếu bỏ qua mọi ma sát thì cơ năng của con lắc đơn được bảo toàn.
W =
mv2
Thế năng: Wt= mgl (1 - cosα)
Cơ năng: Nếu bỏ qua mọi ma sát thì cơ năng của con lắc đơn được bảo toàn.
W =  mv2 + mgl(1 - cosα) = hằng số.
4. Lực kéo về: có độ lớn tỉ lệ với li độ Pt= -mgsinα = -mgα = -mg
mv2 + mgl(1 - cosα) = hằng số.
4. Lực kéo về: có độ lớn tỉ lệ với li độ Pt= -mgsinα = -mgα = -mg 5. Ứng dụng của con lắc đơn
- Dùng để xác định gia tốc rơi tự do trong lĩnh vực địa chất.
- Cách xác định gia tốc rơi tự do (gia tốc trọng trường)
• Đo thời gian gian t của con lắc thực hiện được n dao động toàn phần, sử dụng công thức T =
5. Ứng dụng của con lắc đơn
- Dùng để xác định gia tốc rơi tự do trong lĩnh vực địa chất.
- Cách xác định gia tốc rơi tự do (gia tốc trọng trường)
• Đo thời gian gian t của con lắc thực hiện được n dao động toàn phần, sử dụng công thức T =  để tính chu kì T.
• Sau đó tính gia tốc trọng trường bằng công thức g =
để tính chu kì T.
• Sau đó tính gia tốc trọng trường bằng công thức g =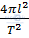 Lặp lại thí nghiệm nhiều lần, rồi tính giá trị trung bình g ở các lần đo, ta được gia tốc rơi tự do tại nơi đó.
B. TRẢ LỜI CÂU HỎI C1, C2, C3 SGK VẬT LÝ 12 BÀI 3
C1. Chứng tỏ rằng đối với những góc lệch nhỏ hơn 20o thì độ chênh lệch giữa sinα và α (rad) không đến 1%.
Trả lời:
Ta kiểm nghiệm với các góc lệch nhỏ bằng 20°, ta có sinα ≃
Lặp lại thí nghiệm nhiều lần, rồi tính giá trị trung bình g ở các lần đo, ta được gia tốc rơi tự do tại nơi đó.
B. TRẢ LỜI CÂU HỎI C1, C2, C3 SGK VẬT LÝ 12 BÀI 3
C1. Chứng tỏ rằng đối với những góc lệch nhỏ hơn 20o thì độ chênh lệch giữa sinα và α (rad) không đến 1%.
Trả lời:
Ta kiểm nghiệm với các góc lệch nhỏ bằng 20°, ta có sinα ≃ α (α tính bằng radian).
sin20° = 0,3420
20° =
α (α tính bằng radian).
sin20° = 0,3420
20° =  = 0,3491 rad
Do đó độ chênh lệch giữa sinα và α là:
0,3491 - 0,3420= 0,0071 = 0,7%.
C2. Có nhận xét gì về chu là của con lắc đơn?
Trả lời:
Chu kì con lắc T = 2π
= 0,3491 rad
Do đó độ chênh lệch giữa sinα và α là:
0,3491 - 0,3420= 0,0071 = 0,7%.
C2. Có nhận xét gì về chu là của con lắc đơn?
Trả lời:
Chu kì con lắc T = 2π Ta thấy chu kì T phụ thuộc vào chiều dài dây l và gia tốc trọng trường g.
T tỉ lệ với căn bậc hai của chiều dài l và tỉ lệ nghịch căn bậc hai của gia tốc trọng trường g.
T tăng khi chiều dài l tăng hoặc gia tốc trọng trường giảm.
T giảm khi chiều l giảm hoặc gia tốc trọng trường tăng.
C3. Hãy mô tả một cách định tính sự biến đổi năng lượng của con lắc, khi nó đi từ vị trí biên về vị trí cân bằng và khi nó đi từ vị trí cân bằng ra vị trí biên.
Trả lời:
Khi con lắc đi từ vị trí biên về vị trí cân bằng thì: s giảm (thế năng giảm), v tăng (động năng tăng).
Tại vị trí cân bằng: s = 0 (thế năng bằng 0), v cực đại (động năng cực đại)
Khi con lắc đi từ vị trí cân bằng đến vị trí biên: s tăng (thế năng tăng), v giảm (động năng giảm).
Tại vị trí biên: s cực đại (thế năng cực đại), v = 0 (động năng bằng 0).
Vậy: trong quá trình dao động đi từ vị trí biên đến vị trí cân bằng hay đi từ vị trí cân bằng đến vị trí biên, khi động năng tăng thì thế năng giảm và ngược lại.
C. TRẢ LỜI CÂU HỎI VÀ BÀI TẬP SGK VẬT LÝ 12 BÀI 3 TRANG 17
1. Thế nào là con lắc đơn? Khảo sát dao dộng của con lắc đơn về mặt động lực học. Chứng minh rằng khi dao động nhỏ (sinα ≈ α (rad)), dao động của con lắc đơn là dao dộng điều hoà.
Trả lời:
Ta thấy chu kì T phụ thuộc vào chiều dài dây l và gia tốc trọng trường g.
T tỉ lệ với căn bậc hai của chiều dài l và tỉ lệ nghịch căn bậc hai của gia tốc trọng trường g.
T tăng khi chiều dài l tăng hoặc gia tốc trọng trường giảm.
T giảm khi chiều l giảm hoặc gia tốc trọng trường tăng.
C3. Hãy mô tả một cách định tính sự biến đổi năng lượng của con lắc, khi nó đi từ vị trí biên về vị trí cân bằng và khi nó đi từ vị trí cân bằng ra vị trí biên.
Trả lời:
Khi con lắc đi từ vị trí biên về vị trí cân bằng thì: s giảm (thế năng giảm), v tăng (động năng tăng).
Tại vị trí cân bằng: s = 0 (thế năng bằng 0), v cực đại (động năng cực đại)
Khi con lắc đi từ vị trí cân bằng đến vị trí biên: s tăng (thế năng tăng), v giảm (động năng giảm).
Tại vị trí biên: s cực đại (thế năng cực đại), v = 0 (động năng bằng 0).
Vậy: trong quá trình dao động đi từ vị trí biên đến vị trí cân bằng hay đi từ vị trí cân bằng đến vị trí biên, khi động năng tăng thì thế năng giảm và ngược lại.
C. TRẢ LỜI CÂU HỎI VÀ BÀI TẬP SGK VẬT LÝ 12 BÀI 3 TRANG 17
1. Thế nào là con lắc đơn? Khảo sát dao dộng của con lắc đơn về mặt động lực học. Chứng minh rằng khi dao động nhỏ (sinα ≈ α (rad)), dao động của con lắc đơn là dao dộng điều hoà.
Trả lời:
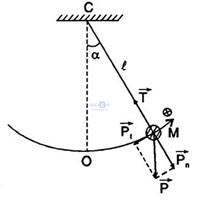 Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu một sợi dây không dãn, khối lượng không đáng kể, dài l.
Khảo sát con lắc về mặt động lực học:
Xét con lắc đơn như hình vẽ:
- Từ vị trí cân bằng kéo nhẹ quả cầu lệch khỏi vị trí cân bằng một góc nhỏ rồi thả ra. Con lắc dao động quanh vị trí cân bằng.
- Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng từ trái sang phải.
- Tại vị trí M bất kì vật m được xác định bởi li độ góc α =
Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu một sợi dây không dãn, khối lượng không đáng kể, dài l.
Khảo sát con lắc về mặt động lực học:
Xét con lắc đơn như hình vẽ:
- Từ vị trí cân bằng kéo nhẹ quả cầu lệch khỏi vị trí cân bằng một góc nhỏ rồi thả ra. Con lắc dao động quanh vị trí cân bằng.
- Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng từ trái sang phải.
- Tại vị trí M bất kì vật m được xác định bởi li độ góc α =  hay về li độ cong là s =
hay về li độ cong là s =  = 1α.
Lưu ý: α, s có giá trị dương khi lệch khỏi vị trí cân bằng theo chiều dương và ngược lại.
- Tại vị trí M, vật chịu tác dụng trọng lực
= 1α.
Lưu ý: α, s có giá trị dương khi lệch khỏi vị trí cân bằng theo chiều dương và ngược lại.
- Tại vị trí M, vật chịu tác dụng trọng lực 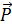 và lực căng
và lực căng 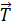 •
• 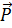 được phân tích thành 2 thành phần:
được phân tích thành 2 thành phần: 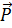 n theo phương vuông góc với đường đi,
n theo phương vuông góc với đường đi, 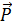 t theo phương tiếp tuyến với quỹ đạo.
• Lực căng T và thành phần
t theo phương tiếp tuyến với quỹ đạo.
• Lực căng T và thành phần 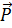 n vuông góc với đường đi nên không làm thay đổi tốc độ của vật.
Thành phần lực
n vuông góc với đường đi nên không làm thay đổi tốc độ của vật.
Thành phần lực 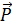 t là lực kéo về có giá trị Pt = -mgsinα (3.1)
Nếu li độ góc a nhỏ thì sinα ≈ a (rad) thì Pt = -mgα = -mg
t là lực kéo về có giá trị Pt = -mgsinα (3.1)
Nếu li độ góc a nhỏ thì sinα ≈ a (rad) thì Pt = -mgα = -mg  so sánh với lực kéo về của con lắc lò xo F= -kx.
Ta thấy có vai trò của k =>
so sánh với lực kéo về của con lắc lò xo F= -kx.
Ta thấy có vai trò của k =>  =
=  Vậy khi dao động nhỏ (sinα ≈ a (rad)), con lắc đơn dao động điều hòa phương trình s = s0cos(ωt + φ).
2. Viết công thức tính chu kì của con lắc đơn khi dao động nhỏ.
Trả lời:
Chu kì dao động của con lắc đơn khi dao động nhỏ T = 2π
Vậy khi dao động nhỏ (sinα ≈ a (rad)), con lắc đơn dao động điều hòa phương trình s = s0cos(ωt + φ).
2. Viết công thức tính chu kì của con lắc đơn khi dao động nhỏ.
Trả lời:
Chu kì dao động của con lắc đơn khi dao động nhỏ T = 2π 3. Viết biểu thức của động năng, thế năng và ca năng của con lắc đơn ở vị trí có góc lệch α bất kì.
Khi con lắc dao động thì động năng và thế năng của con lắc biến thiên như thế nào?
Trả lời:
Động năng của con lắc tại vị trí góc lệch α bất kì Wđ=
3. Viết biểu thức của động năng, thế năng và ca năng của con lắc đơn ở vị trí có góc lệch α bất kì.
Khi con lắc dao động thì động năng và thế năng của con lắc biến thiên như thế nào?
Trả lời:
Động năng của con lắc tại vị trí góc lệch α bất kì Wđ=  mv2
Thế năng của con lắc tại vị trí góc lệch α bất kì Wt = mgl (1 - cosα) (mốc tính thế năng tại vị trí cân bằng).
Cơ năng: Nếu bỏ qua mọi ma sát thì cơ năng của con lắc đơn được bảo toàn.
W =
mv2
Thế năng của con lắc tại vị trí góc lệch α bất kì Wt = mgl (1 - cosα) (mốc tính thế năng tại vị trí cân bằng).
Cơ năng: Nếu bỏ qua mọi ma sát thì cơ năng của con lắc đơn được bảo toàn.
W =  mv2 + mgl(1 - cosα) = hằng số.
Khi con lắc dao động khi động năng tăng thì thế năng giảm và ngược lại.
4. Hãy chọn câu đúng.
Chu kì của con lắc đơn dao động nhỏ (sin α = α (rad)) là:
A. T =
mv2 + mgl(1 - cosα) = hằng số.
Khi con lắc dao động khi động năng tăng thì thế năng giảm và ngược lại.
4. Hãy chọn câu đúng.
Chu kì của con lắc đơn dao động nhỏ (sin α = α (rad)) là:
A. T = 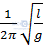 B. T =
B. T = 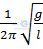 C. T = 2π
C. T = 2π Trả lời:
Đáp án: D
5. Hãy chọn câu đúng.
Một con lắc đơn dao dộng với biên độ góc nhỏ. Chu kì của con lắc không thay đổi khi:
A. Thay đổi chiều dài cửa con lắc.
B. Thay đổi gia tốc trọng trường,
C. Tăng biên độ góc đến 30o.
D. Thay đổi khối lượng của con lắc.
Trả lời:
Đáp án: D
Chu kì của con lắc đơn phụ thuộc vào l, g và biên độ góc không phụ thuộc vào khối lượng m. T không đổi khi thay đổi khối lượng m của con lắc.
6. Một con lắc đơn được thả không vận tốc dầu từ li độ góc α0. Khi con lắc đi qua vị trí cân bằng thì tốc độ của quả cầu con lắc là bao nhiêu?
A.
Trả lời:
Đáp án: D
5. Hãy chọn câu đúng.
Một con lắc đơn dao dộng với biên độ góc nhỏ. Chu kì của con lắc không thay đổi khi:
A. Thay đổi chiều dài cửa con lắc.
B. Thay đổi gia tốc trọng trường,
C. Tăng biên độ góc đến 30o.
D. Thay đổi khối lượng của con lắc.
Trả lời:
Đáp án: D
Chu kì của con lắc đơn phụ thuộc vào l, g và biên độ góc không phụ thuộc vào khối lượng m. T không đổi khi thay đổi khối lượng m của con lắc.
6. Một con lắc đơn được thả không vận tốc dầu từ li độ góc α0. Khi con lắc đi qua vị trí cân bằng thì tốc độ của quả cầu con lắc là bao nhiêu?
A. 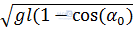 B.
B. 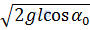 C.
C. 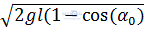 D.
D. 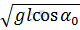 Trả lời:
Đáp án: C
Dùng định luật bảo toàn cơ năng, tại biên và tại vị trí cân bằng.
Tại biên: Wt = mgl(1 – cosα0)
Tại vị trí cân bằng:
Wđ=
Trả lời:
Đáp án: C
Dùng định luật bảo toàn cơ năng, tại biên và tại vị trí cân bằng.
Tại biên: Wt = mgl(1 – cosα0)
Tại vị trí cân bằng:
Wđ=  mv2
Định luật bảo toàn cơ năng:
mv2
Định luật bảo toàn cơ năng:
 mv2= mgl(1 – cosα0) => v =
mv2= mgl(1 – cosα0) => v = 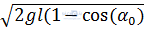 7. Một con lắc đơn dài l = 2,00m, dao động điều hoà tại một nơi có gia tốc rơi tự do g = 9,80 m/s2. Hỏi con lắc thực hiện được bao nhiêu dao động toàn phần trong 5,00 phút?
Giải:
Chu kì dao động T = 2π
7. Một con lắc đơn dài l = 2,00m, dao động điều hoà tại một nơi có gia tốc rơi tự do g = 9,80 m/s2. Hỏi con lắc thực hiện được bao nhiêu dao động toàn phần trong 5,00 phút?
Giải:
Chu kì dao động T = 2π = 2π
= 2π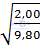 => T = 2,84(s)
Số dao động toàn phần trong 5 phút:
T =
=> T = 2,84(s)
Số dao động toàn phần trong 5 phút:
T =  => n =
=> n =  =
= 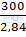 => n = 106 dao động toàn phần.
=> n = 106 dao động toàn phần.
Bản quyền bài viết thuộc về
Sachgiai.com. Ghi nguồn Sách giải.com khi đăng lại bài viết này.