1. Nhân đơn thức với đa thức
Luyện tập 1 trang 19: Nhân hai đơn thức:
a) 3x2 và 2x3;
b) –xy và 4z3;
c) 6xy3 và –0,5x2.
Giải:
a) 3x2 . 2x3 = (3. 2)(x2 . x3) = 6x5;
b) –xy . 4z3 = –4xyz3;
c) 6xy3 . (–0,5x2) = [6 . (–0,5)] (x . x2) y3 = –3x3y3
Hoạt động 1 trang 19: Hãy nhớ lại quy tắc nhân đơn thức với đa thức trong trường hợp chúng có một biến bằng cách thực hiện phép nhân (5x2) . (3x2 – x – 4).
Giải:
Ta có (5x2) . (3x2 – x – 4) = 5x2 . 3x2 – 5x2 . x – 5x2 . 4
= 15x4 – 5x3 – 20x2.
Hoạt động 2 trang 20: Bằng cách tương tự, hãy làm phép nhân (5x2y) . (3x2y – xy – 4y).
Giải:
Ta có (5x2y) . (3x2y – xy – 4y)
= 5x2y . 3x2y – 5x2y . xy – 5x2y . 4y
= (5.3)(x2.x2)(y.y) – 5(x2.x)(y.y) – (5.4)x2(y.y)
= 15x4y2 – 5x3y2 – 20x2y2.
Luyện tập 2 trang 20: Làm tính nhân:
a) (xy) . (x2 + xy – y2);
b) (xy + yz + zx) . (–xyz).
Giải:
a) (xy) . (x2 + xy – y2) = xy . x2 + xy . xy – xy . y2
= x3y + x2y2 – xy3.
b) (xy + yz + zx) . (–xyz) = xy . (–xyz) + yz . (–xyz) + zx . (–xyz)
= –x2y2z – xy2z2 – x2yz2.
Vận dụng trang 20: Rút gọn biểu thức x3(x + y) – x(x3 + y3).
Giải:
Ta có x3(x + y) – x(x3 + y3) = x3 . x + x3 . y – x . x3 – x . y3
= x4 + x3y – x4 – xy3 = x3y – xy3.
2. Nhân đa thức với đa thức
Hoạt động 3 trang 20: Hãy nhớ lại quy tắc nhân hai đa thức một biến bằng cách thực hiện phép nhân: (2x + 3) . (x2 – 5x + 4).
Giải:
Ta có (2x + 3) . (x2 – 5x + 4)
= 2x . x2 – 2x . 5x + 2x . 4 + 3 . x2 – 3 . 5x + 3 . 4
= 2x3 – 10x2 + 8x + 3x2 – 15x + 12
= 2x3 + (3x2 – 10x2) + (8x – 15x) + 12
= 2x3 – 7x2 – 7x + 12.
Hoạt động 4 trang 20: Bằng cách tương tự, hãy thử làm phép nhân (2x + 3y) . (x2 – 5xy + 4y2).
Giải:
Ta có (2x + 3y) . (x2 – 5xy + 4y2)
= 2x . x2 – 2x . 5xy + 2x . 4y2 + 3y . x2 – 3y . 5xy + 3y . 4y2
= 2x3 – 10x2y + 8xy2 + 3x2y – 15xy2 + 12y3
= 2x3 + 12y3 + (3x2y – 10x2y) + (8xy2 – 15xy2)
= 2x3 + 12y3 – 7x2y – 7xy2.
Luyện tập 3 trang 21: Thực hiện phép nhân:
a) (2x + y)(4x2 – 2xy + y2);
b) (x2y2 – 3)(3 + x2y2).
Giải:
a) (2x + y)(4x2 – 2xy + y2)
= 2x . 4x2 – 2x . 2xy + 2x . y2 + y . 4x2 – y . 2xy + y . y2
= 8x3 – 4x2y + 2xy2 + 4x2y – 2xy2 + y3
= 8x3 + (4x2y – 4x2y) + (2xy2 – 2xy2) + y3
= 8x3 + y3.
b) (x2y2 – 3)(3 + x2y2) = x2y2 . 3 + x2y2 . x2y2 – 3 . 3 – 3 . x2y2
= 3x2y2 + x4y4 – 9 – 3x2y2 = x4y4 – 9.
Thử thách nhỏ trang 21: Xét biểu thức đại số với hai biến k và m sau: P = (2k – 3)(3m – 2) – (3k – 2)(2m – 3).
a) Rút gọn biểu thức P.
b) Chứng minh rằng tại mọi giá trị nguyên của k và m, giá trị của biểu thức P luôn là một số nguyên chia hết cho 5.
Giải:
a) P = (2k – 3)(3m – 2) – (3k – 2)(2m – 3)
= (6km – 9m – 4k + 6) – (6km – 4m – 9k + 6)
= 6km – 9m – 4k + 6 – 6km + 4m + 9k – 6
= (6km – 6km) + (4m – 9m) + (9k – 4k) + (6 – 6) = 5k – 5m.
b) Ta thấy P = 5k – 5m = 5(k – m)
Vì 5 ⋮ 5 nên 5(k – m) ⋮ 5
Do đó, tại mọi giá trị nguyên của k và m, giá trị của biểu thức P luôn là một số nguyên chia hết cho 5.
3. Giải Bài tập trang 21
Bài 1.24: Nhân hai đơn thức:
a) 5x2y và 2xy2;
b)  xy và 8x3y2;
xy và 8x3y2;
c) 1,5xy2z3 và 2x3y2z.
Giải:
a) 5x2y . 2xy2 = (5. 2)(x2 . x)(y . y2) = 10x3y3;
b)  xy . 8x3y2 =
xy . 8x3y2 = 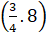
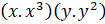 = 6x4y3;
= 6x4y3;
c) 1,5xy2z3 . 2x3y2z = (1,5 . 2)(x . x3)(y2 . y2)(z . z3) = 3x4y4z4.
Bài 1.25: Tìm tích của đơn thức với đa thức:

Giải:

Bài 1.26: Rút gọn biểu thức x(x2 – y) – x2(x + y) + xy(x – 1).
Giải:
Ta có x(x2 – y) – x2(x + y) + xy(x – 1)
= x . x2 – x . y – x2 . x – x2 . y + xy . x – xy . 1
= x3 – xy – x3 – x2y + x2y – xy
= (x3 – x3) + (x2y – x2y) – (xy + xy) = –2xy.
Bài 1.27: Làm tính nhân:

Giải:

Bài 1.28: Rút gọn biểu thức sau để thấy rằng giá trị của nó không phụ thuộc vào giá trị của biến: (x - 5)(2x + 3) - 2x(x - 3) + x + 7
Giải:
Ta có (x – 5)(2x + 3) – 2x(x – 3) + x + 7
= x . 2x + x . 3 – 5 . 2x – 5 . 3 – 2x . x + 2x . 3 + x + 7
= 2x2 + 3x – 10x – 15 – 2x2 + 6x + x + 7
= (2x2 – 2x2) + (3x – 10x + 6x + x) + (7 – 15)
= –8.
Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.
Bài 1.29: Chứng minh đẳng thức sau: (2x + y)(2x2 + xy – y2) = (2x – y)(2x2 + 3xy + y2).
Giải:
Ta có:
• (2x + y)(2x2 + xy – y2)
= 2x . 2x2 + 2x . xy – 2x . y2 + y . 2x2 + y . xy – y . y2
= 4x3 + 2x2y – 2xy2 + 2x2y + xy2 – y3
= 4x3 + (2x2y + 2x2y) + (xy2 – 2xy2) – y3
= 4x3 + 4x2y – xy2 – y3.
• (2x – y)(2x2 + 3xy + y2)
= 2x . 2x2 + 2x . 3xy + 2x . y2 – y . 2x2 – y . 3xy – y . y2
= 4x3 + 6x2y + 2xy2 – 2x2y – 3xy2 – y3
= 4x3 + (6x2y – 2x2y) + (2xy2 – 3xy2) – y3
= 4x3 + 4x2y – xy2 – y3.
Do đó (2x + y)(2x2 + xy – y2) = (2x – y)(2x2 + 3xy + y2) = 4x3 + 4x2y – xy2 – y3.
Vậy (2x + y)(2x2 + xy – y2) = (2x – y)(2x2 + 3xy + y2).