Bài 30 (SGK trang 16 Toán lớp 8 tập 1)
Rút gọn các biểu thức sau:
a) (x + 3)(x2 – 3x + 9) – (54 + x3)
b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
Giải:
a) (x + 3)(x2 – 3x + 9) – (54 + x3) = (x + 3)(x2 – 3x + 32) – (54 + x3)
= x3 + 33 – (54 + x3)
= x3 + 27 – 54 – x3
= -27
b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
= (2x + y)[(2x)2 – 2 . x . y + y2] – (2x – y)(2x)2 + 2 . x . y + y2]
= [(2x)3 + y3]- [(2x)3 – y3]
= (2x)3 + y3– (2x)3 + y3= 2y3
Bài 31 (SGK trang 16 đại số 8 tập 1)
Chứng minh rằng:
a) a3 + b3 = (a + b)3 – 3ab(a + b)
b) a3 – b3 = (a – b)3 + 3ab(a – b)
Áp dụng: Tính a3 + b3, biết a . b = 6 và a + b = -5
Giải:
a) a3 + b3 = (a + b)3 – 3ab(a + b)
Thực hiện vế phải:
(a + b)3 – 3ab(a + b) = a3 + 3a2b+ 3ab2 + b3 – 3a2b – 3ab2
= a3 + b3
Vậy a3 + b3 = (a + b)3 – 3ab(a + b)
b) a3 – b3 = (a – b)3 + 3ab(a – b)
Thực hiện vế phải:
(a – b)3 + 3ab(a – b) = a3 – 3a2b+ 3ab2 – b3 + 3a2b – 3ab2
= a3 – b3
Vậy a3 – b3 = (a – b)3 + 3ab(a – b)
Áp dụng:
Với ab = 6, a + b = -5, ta được:
a3 + b3 = (a + b)3 – 3ab(a + b) = (-5)3 – 3 . 6 . (-5)
= -53 + 3.6.5 = -125 + 90 = -35.
Bài 32 (SGK trang 16 Toán lớp 8 tập 1)
Điền các đơn thức thích hợp vào ô trống:
a) (3x + y)(☐-☐+☐) = 27x3 + y3
b) (2x -☐)(☐- 10x +☐) = 8x3 -125
Giải:
a) Ta có: 27x3 + y3 = (3x)3 + y3= (3x + y)[(3x)2 – 3x.y + y2] = (3x + y)(9x2 – 3xy + y2)
Nên: (3x + y) (9x2 – 3xy + y2) = 27x3 + y3
b) Ta có: 8x3 – 125 = (2x)3 – 53= (2x – 5)[(2x)2 + 2x . 5 + 52]
= (2x – 5)(4x2 + 10x + 25)
Nên:(2x – 5)(4x2 + 10x + 25)= 8x3 – 125
Bài 33 (SGK trang 16 Toán lớp 8 tập 1)
a) (2 + xy)2 b) (5 – 3x)2
c) (5 – x2)(5 + x2) d) (5x – 1)3
e) (2x – y)(4x2 + 2xy + y2) f) (x + 3)(x2 – 3x + 9)
Giải:
a) (2 + xy)2 = 22 + 2.2.xy + (xy)2 = 4 + 4xy + x2y2
b) (5 – 3x)2= 52 – 2.5.3x + (3x)2 = 25 – 30x + 9x2
c) (5 – x2)(5 + x2) = 52 – (x2)2 = 25 – x4
d) (5x – 1)3 = (5x)3 – 3.(5x)2. 1 + 3.5x.12 – 13 = 125x3 – 75x2 + 15x – 1
e) (2x – y)(4x2 + 2xy + y2) = (2x – y)[(2x)2 + 2x . y + y2] = (2x)3 – y3 = 8x3 – y3
f) (x + 3)(x2 – 3x + 9) = (x + 3)(x2 – 3x + 32) = x3 + 33 = x3 + 27.
Bài 34: (SGK trang 17 đại số 8 tập 1)
Rút gọn các biểu thực sau:
a) (a + b)2 – (a – b)2; b) (a + b)3 – (a – b)3 – 2b3
c) (x + y + z)2 – 2(x + y + z)(x + y) + (x + y)2
Giải:
a) (a + b)2 – (a – b)2 = (a2 + 2ab + b2) – (a2 – 2ab + b2)
= a2 + 2ab + b2 – a2 + 2ab – b2 = 4ab
Hoặc (a + b)2 – (a – b)2 = [(a + b) + (a – b)][(a + b) – (a – b)]
= (a + b + a – b)(a + b – a + b) = 2a . 2b = 4ab
b) (a + b)3 – (a – b)3 – 2b3
= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3) – 2b3
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3 – 2b3 = 6a2b
Hoặc (a + b)3 – (a – b)3 – 2b3 = [(a + b)3 – (a – b)3] – 2b3
= [(a + b) – (a – b)][(a + b)2 + (a + b)(a – b) + (a – b)2] – 2b3
= (a + b – a + b)(a2 + 2ab + b2 + a2 – b2 + a2 – 2ab + b2) – 2b3
= 2b.(3a2 + b2) – 2b3 = 6a2b + 2b3 – 2b3 = 6a2b
c) (x + y + z)2 – 2(x + y + z)(x + y) + (x + y)2
= x2 + y2 + z2+ 2xy + 2yz + 2xz – 2(x2 + xy + yx + y2 + zx + zy) + x2 + 2xy + y2
= 2x2 + 2y2 + z2 + 4xy + 2yz + 2xz – 2x2 – 4xy – 2y2 – 2xz – 2yz = z2
Bài 35: (SGK trang 17 đại số 8 tập 1)
Tính nhanh:
a) 342 + 662 + 68 . 66; b) 742 + 242 – 48 . 74.
Giải:
a) 342 + 662 + 68 . 66 = 342 + 2.34.66 + 662 = (34 + 66)2 = 1002 = 10000.
b) 742 + 242 – 48.74 = 742 – 2.74.24 + 242 = (74 – 24)2= 502 = 2500
Bài 36: (SGK trang 17 đại số tập 1)
Tính giá trị của biểu thức:
a) x2 + 4x + 4 tại x = 98; b) x3 + 3x2 + 3x + 1 tại x = 99
Giải:
a) x2 + 4x + 4 = x2 + 2.x.2 + 22 = (x+ 2)2
Với x = 98: (98+ 2)2 =1002 = 10000
b) x3 + 3x2 + 3x + 1 = x3 + 3.1.x2 + 3.x .12+ 13 = (x + 1)3
Với x = 99: (99+ 1)3 = 1003 = 1000000
Bài 37: (SGK trang 17 đại số 8 tập 1)
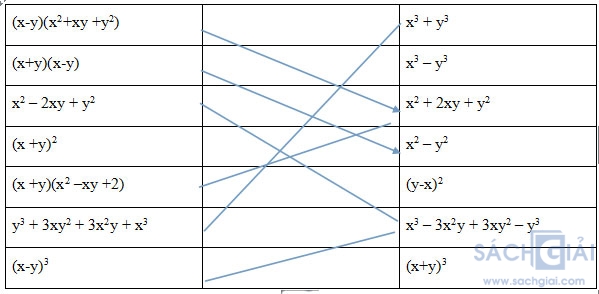
Dùng bút chì nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu)
| (x-y)(x2+xy +y2) | | x3 + y3 |
| (x+y)(x-y) | | x3 – y3 |
| x2 – 2xy + y2 | | x2 + 2xy + y2 |
| (x +y)2 | | x2 – y2 |
| (x +y)(x2 –xy +2) | | (y-x)2 |
| y3 + 3xy2 + 3x2y + x3 | | x3 – 3x2y + 3xy2 – y3 |
| (x-y)3 | | (x+y)3 |
Giải:
Ta có: (x – y)(x2 + xy + y2) = X3 – y3 và (x + y)(x2 – xy + y2) = X3 + y3
(x + y) (x – y) = X2 – y2 và X2 – 2xy + y2 = (x – y)2 = (y – x)2 y3 + 3xy2 + 3x2y + X3 = (y + x)3 = (x + y)3 và (x + y)2 = X2 + 2xy + y2 (x – y)3 = X3 – 3x2y + 3xy2 – y3
Từ đó ta có:
Bài 38: (SGK trang 17 đại số 8 tập 1)
Chứng minh các đẳng thức sau:
a) (a – b)3 = -(b – a)3; b) (- a – b)2 = (a + b)2
Giải:
a) (a – b)3 = -(b – a)3
Biến đổi vế phải thành vế trái:
-(b – a)3= -(b3 – 3b2a + 3ba2 – a3) = – b3 + 3b2a – 3ba2 + a3
= a3 – 3a2b + 3ab2 – b3 = (a – b)3
Sử dụng tính chất hai số đối nhau:
(a – b)3 = [(-1)(b – a)]3 = (-1)3(b – a)3 = -13.(b – a)3 = – (b – a)3
b) (- a – b)2 = (a + b)2
Biến đổi vế trái thành vế phải:
(- a – b)2 = [(-a) + (-b)]2
= (-a)2 +2.(-a).(-b) + (-b)2
= a2 + 2ab + b2 = (a + b)2
Sử dụng tính chất hai số đối nhau:
(-a – b)2 = [(-1) . (a + b)]2 = (-1)2 . (a + b)2 = 1 . (a + b)2 = (a + b)2